There's always a circle through three given points, as long as they're not on a line. Circles through four given points - those are exceptional. Especially when the four points are well-known special points of a triangle.
Theorem: If a triangle has no two sides equal, there is a circle passing through the following four special points:
- its circumcentre C
- its nine-point centre N
- its first Fermat point F
- its second Fermat point S.
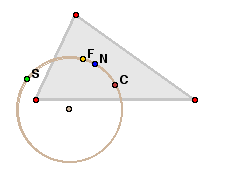
Furthermore, the points always occur around the circle in that order: C-N-F-S (either clockwise or counterclockwise).
This circle attracted attention after its discovery was publicized by Clark Kimberling, who first called it the Lester circle (see the paper in the bibliography).
I discovered the circle when I was exploring ways of using complex numbers to study euclidean triangle geometry. The methods that resulted from that exploration produced a large number of very nice examples. This theorem is one of many, but it's my favourite, and the one which provided the motivation for further development of the methods.
The pages of this website are intended to explain interactively what the theorem says and to give some idea of the type of mathematics behind it. There are pages on
- how to construct the four points
- the circle through the four points (all four constructions at once)
- the order of the points around the circle
- the mathematics behind the theorem
- a bibliography of Lester circle material
System requirements. The interactive parts of this website are based on Geometer's Sketchpad applets, and should work in any recent vintage java-enabled browser. They may work in earlier browsers, but those may not display other parts of the pages correctly.
Please report any problems with either the technology or the content to me, .