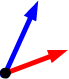
Let's look at what it means geometrically for
a set of two or more vectors to be linearly dependent or linearly independent.
Suppose we have a set of two non-zero vectors.
One is a linear combination of the other whenever it is a scalar multiple of
the other, i.e. whenever it is parallel to the other. Thus:
A set of two vectors is linearly dependent if one is parallel to the other,
and linearly independent if they are not parallel.
(This is true in either 2-space or 3-space.)
Now suppose we have three non-zero vectors, either
in 2-space or in 3-space. There are three possible cases, illustrated for 3-space
below. (The vectors we're discussing are in shades of blue.)
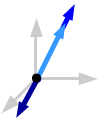
 If any two of the vectors are parallel, then one
is a scalar multiple of the other. A scalar multiple is a linear combination, so the vectors are linearly dependent.
(Notice that all three vectors also lie in a plane.)
If any two of the vectors are parallel, then one
is a scalar multiple of the other. A scalar multiple is a linear combination, so the vectors are linearly dependent.
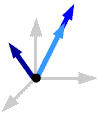
(Notice that all three vectors also lie in a plane.)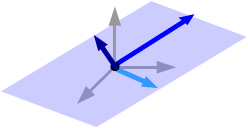 If no two of the vectors are parallel but all
three lie in a plane, then any two of those vectors span that plane. The third
vector is a linear combination of the first two, since it also lies in this
plane, so the vectors are linearly dependent.
If no two of the vectors are parallel but all
three lie in a plane, then any two of those vectors span that plane. The third
vector is a linear combination of the first two, since it also lies in this
plane, so the vectors are linearly dependent.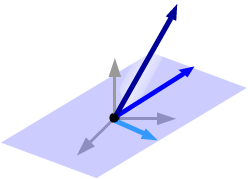
If the three vectors don't all lie in some plane through the origin, none is in the span of the other two, so none is a linear combination of the other two. The three vectors are linearly independent.
Now suppose we have four or more non-zero vectors.
If any three all lie on a line or on a plane, they are clearly linearly dependent,
so the set of all the vectors is linearly dependent. If some three of the
four don't lie on a plane, they span all of 3-space, so the others must be
linear combinations of those three and again, the vectors are linearly dependent.
Thus:
Four or more vectors in 2-space or in 3-space must be linearly dependent.
Here's a summary of how geometric vectors in 2-space or in 3-space can
be linearly independent.
- Two vectors are linearly independent if they are not parallel.
- Three vectors are linearly independent if they don't all lie in a plane.
- More than two vectors in 2-space must be linearly dependent
- More than three vectors in 3-space must be linearly dependent.
 Linear
Independence Linear
Independence |
|||
| Introduction | The basic definition of linear independence | Examples of linearly independent geometric vectors | A more practical form of linear independence |