A linear equation is one like
2x1 – 3x2 + 5x3 + 7x4 – 2x5 = 11
Here, the variables are x1, x2, x3, x4 and x5, and on the left, you have sums and differences of (constant)x(variable) terms – no powers or products or other complications. Linear equations generally come in systems of several equations in the same variables, for example:
|
2x1 – 3x2 + 5x3 + 7x4 – 2x5 |
= 11 |
|
3x1 – x2 + 5x3 – 2x4 + x5 |
= –3 |
|
x1 – 2x2 + 4x3 – 6x4 – x5 |
= 7 |
|
–4x1 – 3x2 + 4x3 + 9x4 + 5x5 |
= 13 |
The first key idea for solving linear systems: save writing.
Instead of copying down all the variables over again each time you operate on the system, work only with the numbers – the coefficients of the variables and the constants on the right. Put those numbers into their corresponding positions in a rectangular array of numbers (the augmented matrix of the system) and operate on the rows of that matrix instead of on the corresponding equations.
The second key idea: decide clearly what it is you're allowed to do to the augmented matrix to solve the system. Without the matrix, you'd multiply equations by constants or add them to other equations, for example. With the augmented matrix, you'll do similar operations on its rows: the elementary row operations.
|
Elementary row operation |
Notation |
|
|
|
|
|
|
Note the notation: it's a good idea to keep a record of the row operations you use to solve a system, both to check your work afterward and to inform anyone else trying to follow your work what it is you're doing. Read the back arrow "←" as "is replaced by" and the double arrow "↔" as "is exchanged with".
Another important point: the matrix that results from applying row operations to another matrix is not equal to the original matrix, so don't put an "=" sign between them. Matrices are equal only when they are identical, with exactly the same numbers in every position. Matrices which are related by one or more row operations are called row equivalent. If you want, you can use the symbol "~" to indicate row equivalence.
Once you've used elementary row operations to transform the augmented matrix into as simple a form as possible, you then translate the matrix back into a system of equations and write down the solutions. Here's a flowchart summarizing the complete process.
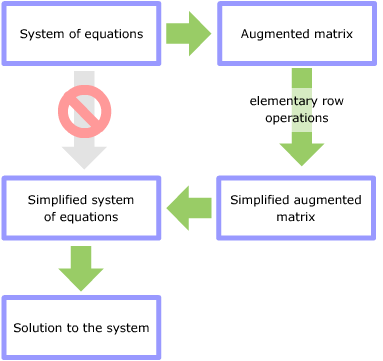
The next steps are to fill in the details of his process. You need to know: