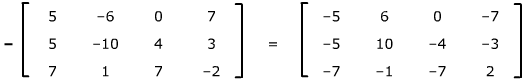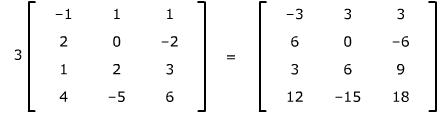Matrix addition, subtraction and scalar multiplication
Matrices can be added or subtracted only when they have the same size. The
relevant definitions:
To add or subtract
two m x n matrices, add or subtract their corresponding entries.

|
The negative of a matrix
is the matrix whose entries are the negatives of the original matrix.
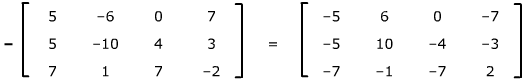
|
A zero matrix is one of
any size all of whose entries are 0. Notation: Omn
if it's important to indicate the size, O
if the size is unimportant or clear from the context.

|
The word "scalar" just means "number" – we use a
separate word to distinguish numbers from other mathematical objects we want
to calculate with, like matrices.
To multiply a matrix by a scalar, multiply every entry of the matrix
by that scalar.
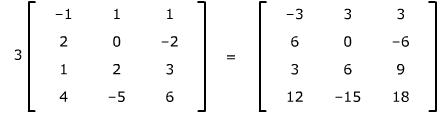
|
You can derive most of the calculation rules for matrix addition, subtraction
and scalar multiplication from the rules for addition, subtraction and multiplication
of ordinary numbers. Here is a list of ten rules that are considered to be "essential"
for matrix addition and scalar multiplication.
| Ten Essential Rules for m x n Matrices |
| Closure rules:
for m x n matrices A and B
and any scalar c, |
A + B
is an m x n matrix
|
cA is an m x n matrix
|
| Arithmetic rules for addition:
for any m x n matrices A, B
and C, |
A + B
= B + A
|
A + (B
+ C) = (A
+ B) + C
|
There is an m x n matrix Omn
such that A + Omn
= Omn
+ A = A
for all m x n matrices A.
|
For each m x n matrix A, there is
an m x n matrix –A such that
A + (–A)
= O.
|
| Arithmetic rules for scalar multiplication:
for any m x n matrices A and B
and any scalars c and d, |
c(A + B)
= cA + cB
|
(c + d)A = cA
+ dA
|
(cd)A = c(dA)
|
1A = A
|
Why are these rules "essential"? After all, they're all pretty obvious
– the last says that multiplying a matrix by the scalar 1 doesn't change
the matrix, for example - and other obvious rules such as 0A
= Omn are
not on the list.
The point is, the rules in the list are very basic mathematical properties
shared with other types of mathematical objects - it's the rules themselves
that are important, not the objects that obey them. You'll see how all this
works out later on in the course; for now, just make sure you understand what
those rules say.
If you take an extended combination of sums and scalar multiples of matrices
of the same size, you get what is called a linear combination.
A linear combination of
several matrices A1,
A2, ..., Ak
of the same size is any matrix of the form
c1A1
+ c2A2
+ ... + ckAk
where c1, c2,
..., ck are all scalars.
|
For example, if A, B,
C and D are
all 2 x 3 matrices, then the 2 x 3 matrix 3A
– 2B – 5C
+ D is a linear combination of A,
B, C and D.
So is 3(A + 2B)
– 4C + 5(D
– A + C)
– B, since you can use the ten rules
to simplify this expression to –2A +
5B + C + 5D.