Spans
In linear algebra, the word span can be both a noun and a verb.
As a noun, the span of a set
of vectors is the set of all linear combinations of those vectors.
Since sums and scalar products of linear combinations of vectors are
themselves linear combinations of those same vectors, the span of a
collection of vectors is a subspace of the vector space those vectors
came from.
|
Conversely, if all the vectors in a vector space are linear combinations
of a certain finite collection of vectors, then we say that the vectors
of that collection span the space
– here, span is a verb.
|
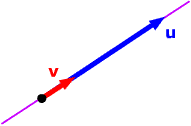
: the span of two
geometric vectors u and v
in two-dimensional Euclidean space.
There are two possibilities: either u and
v are parallel or they are not.
If u
and v are parallel, any linear combination
of them is also parallel to both. Any vector parallel to both is a scalar
multiple of either, and is thus a linear combination of u
and v. So the subspace spanned by the
parallel vectors u and v
is the line through the origin containing them.
|
|
| |
|
If u and
v are not parallel, look at any other
vector w in the plane.
|
| |
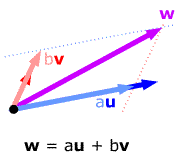
Draw lines through the tip of w
parallel to u and v.
These lines and the lines of u and v
form a parallelogram. The vectors along the sides of this parallelogram
through the origin are scalar multiples of u
and v, and these scalar multiples sum
to w, i.e. w
is in the span of u and v.
|
|
You can get any
vector w in the plane this way, so the
subspace spanned by u and v
is the whole plane.
|
More generally, if you have two vectors in three-dimensional
Euclidean space, their span is still the line or plane containing them.
If you have three or more vectors in three-dimensional Euclidean space, the
possibilities are
- they are all parallel, in which case their span is the line through the
origin containing them
- they are not all parallel, but all lie in some plane through the origin,
in which case their span is that plane
- they do not lie in any one plane through the origin, in which case their
span is the whole of the space.
You should check these statements by drawing pictures.
:
The elementary vectors in Rn
span all of Rn.
|
| The matrices
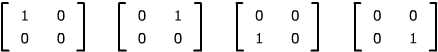
span the vector space of 2 x 2 matrices, since any 2 x 2 matrix 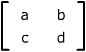 can be written as
can be written as
 . .
|
The polynomials 1, x, x2,
x3, ..., xn
span the vector space of polynomials of degree n or less.
|
| To determine whether or not a set of vectors
spans a vector space |
Given a set of vectors {v1,
v2,
..., vk}
in a vector space:
|
Set up the equation
c1v1
+ c2v2
+ ... + ckvk
= b
where b is a generic vector in the
space.
|
If possible, find a solution c1,
c2, ..., ck
for this equation.
|
If there is a solution for every possible vector b,
then the set {v1,
v2,
..., vk}
spans the space.
|
If there is no solution for
some vector b, the set {v1,
v2,
..., vk}
does not span the space.
|

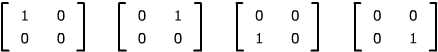
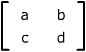 can be written as
can be written as  .
.