Orthogonal complements

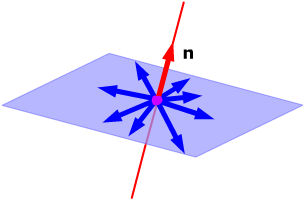
Suppose you have a 2-dimensional subspace of Euclidean 3-space, i.e. a plane through the origin with some normal vector n. All the vectors in 3-space orthogonal to this plane must then be parallel to n, so they form a 1-dimensional subspace of 3-space.

This sort of relationship also works in general inner product spaces - the vectors orthogonal to all vectors in one subspace always form another subspace.

If W is a subspace of an inner product space V, then the set of vectors orthogonal to all vectors in W is also a subspace of V.

Proof. This is easy to check: look at the closure rules.

If u and v are orthogonal to all vectors in W , then for every vector w in W,
[u + v, w] = [u, w] + [v, w] = 0 + 0 = 0,
so u + v is also orthogonal to all vectors in W.

If u is a vector orthogonal to all vectors in W, then for every vector w in W and any scalar k,
[ku, w] = k[u, w] = k0 = 0,
so ku is also orthogonal to all vectors in W.

This new subspace has a name.

The subspace of vectors orthogonal to a subspace W of an inner product space V is called the orthogonal complement of W, and is denoted by W⊥, read "W perp".

The word "complement" comes from the fact that the subspace W⊥ "complements" the subspace W, in the sense that both together give you all of V. More precisely:

If W is a subspace of an inner product space V, then any vector v in V can be written as v = w + w⊥, where w is a vector in W and w⊥ is a vector in W⊥.

Proof. (omitted)

Some other properties of orthogonal complements.

If W is a subspace of an inner product space V, then

W∩W⊥ = {0}

Proof. Any vector in both W and W⊥ must be orthogonal to itself. The only vector orthogonal to itself is the zero vector.

If V is finite-dimensional, then (W⊥)⊥ = W.

Proof. (omitted)

If V is finite-dimensional, then dimW + dimW⊥ = dimV.

Proof. (omitted)

Though orthogonality is essentially a geometric concept, there's a connection between orthogonal complements and the fundamental subspaces of a matrix.

The null space and the row space of any m x n matrix A are orthogonal complements of each other with respect to the Euclidean inner product on Rn.

Proof. Denote the rows of A by r1, r2, ..., rm. Any vector w in the row space of A i s a linear combination of r1, r2, ..., rm:

w = c1r1 + c2r2 + ... + cmrm.

A vector x is in the null space of A if and only if it satisfies Ax = 0, so (since the multiplication Ax is the dot product of x with the rows of A), x is in the null space of A if and only if it is orthogonal to all the rows r1, r2, ..., rm. Then

[x, w]

= [x, c1r1 + c2r2 + ... + cmrm]
= c1[x, r1] + c2[x, r2] + ... + c1[x, r2]
= 0.

Thus x is in the null space of A if and only if it is orthogonal to every vector in the row space of A. This says that the null space of A is the orthogonal complement of the row space of A.

This last result can be used to find a basis of an orthogonal complement of a subspace of Rn if you are given a basis of the space itself.

To find a basis of an orthogonal complement in Rn

Given a basis {b1, b2, ..., bm} of a subspace W of Rn

Form the matrix A with rows b1, b2, ..., bm.

Find a basis of the null space of A

That basis will be a basis of W⊥