Given an arbitrary basis {u1, u2, ..., un} of an inner product space V, construct the vectors v1, v2, ..., vn as follows:
Step 1: take v1 = u1
Step k for k = 2, ..., n: form vk by subtracting from uk its projections on all the previously found v1, v2, ..., vk–1, i.e.
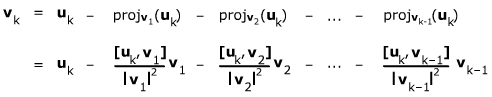
Then {v1, v2, ..., vn} is an orthogonal basis of V.
To construct an orthonormal basis, use the Gram-Schmidt process to find an orthogonal basis and then normalize each of the basis vectors you found.