General linear transformations and their matrices

A linear transformation between two general vector spaces is defined just as we defined a linear transformation between Rm and Rn.

A linear transformation from a vector space V to a vector space W is a function T:V → W which preserves sums and scalar multiples. Specifically, for all vectors u and v in V and all scalars c:

T(u + v) = T(u) + T(v)
T(cu) = cT(u).

Most of what we said earlier about linear transformations still works for these more general linear transformations. The kernel and image are defined just as before, and the discussions of one-one and onto transformations are still valid.

 

In he last section, we represented linear operators on Rn by matrix multiplications of coordinate vectors. We're now going to look at representing general linear transformations by matrix multiplications.

Suppose we have this situation:

 

We want to use coordinates to represent this linear transformation. Suppose we choose bases for both spaces and represent vectors in each space by their coordinates with respect to those bases.

 

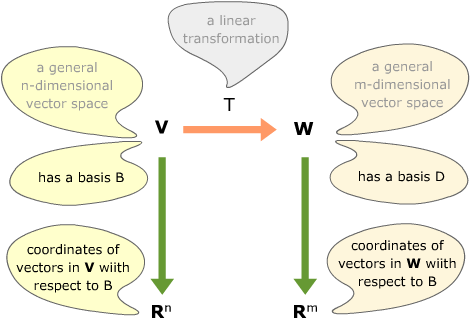
To describe this linear transformation in terms of the coordinates on the two spaces, we want a matrix which multiplies coordinates of vectors in the first space to give the coordinates of their transforms in the second space.

 

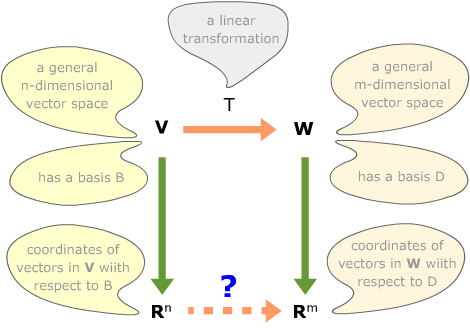
Here's how to find the matrix which represents the transformation between coordinates.

Suppose T:V → W is a linear transformation, B = {b1, b2, ..., bn} is an ordered basis of V and D is an ordered basis of W. Then for all vectors x in V,

[T(x)]D = C[x]B,

where C is the matrix with columns [T(b1)]D, [T(b2)]D, ..., [T(bn)]D.

Proof. (omitted; very much like the proof of the similar theorem in the last section)

 

For any linear transformation T:V → W and any ordered bases B = {b1, b2, ..., bn} of V and D of W , the matrix with columns [T(b1)]D, [T(b2)]D, ..., [T(bn)]D is called the matrix of T with respect to B and D.

 

Example. Suppose that T:P3 → P2 is the linear transformation that differentiates each polynomial. Find the matrix of T with respect to the standard bases on each space, and use it to verify that matrix multiplication of coordinates gives the correct result for p(x) = – 2 + 5x + 3x2.

The standard bases of P3 and P2 are E = {1, x, x2} and F = {1, x} respectively. Then:

T(1) = (1)' = 0 = 0 + 0x,   so   [T(1)]F = [0, 0]T

T(x) = (x)' = 1 = 1 + 0x,   so  [T(x)]F = [1, 0]T

T(x2) = (x2)' = 2x = 0 + 2x,   so  [T(x2)]F = [0, 2]T.

The matrix of the transformation with respect to these two bases is then

The coordinates of p(x) are [p(x)]E = [–2, 5, 3]T, and since p'(x) = 5 + 6x, the coordinates of T(p(x)) are [T(p(x))]F = [5, 6]T. Since

,

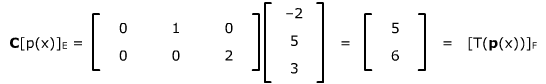the matrix multiplication gives the correct transformation for p(x) = – 2 + 5x + 3x2.