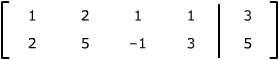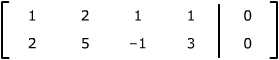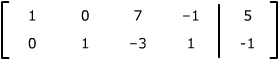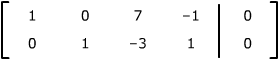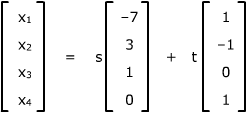Homogeneous systems
A homogeneous linear system
is one of the form Ax
= 0, i.e. one for which the constant
terms on the right are all zero. A homogeneous linear system always
has at least the trivial solution
x = 0.
|
Here's a result that is not true for
non-homogeneous linear systems.
A homogeneous linear system Ax = 0
with more variables than equations must always have infinitely many
solutions.
|
| :
Since A has more columns than rows, the
reduced row-echelon form of [A|0]
has more columns left of the bar than rows, and hence more columns left
of the bar than leading 1's. The solution must then contain parameters,
so there are infinitely many solutions.
|
The solutions of a general linear system Ax
= b and its corresponding homogeneous system
Ax = 0
are related to each other.
Let xp
be any particular solution of the linear system Ax
= b. Then
|
a) For any solution xH
of the homogemeous system Ax = 0, xP
+ xH
is a solution of Ax = b.
|
b) All solutions of Ax = b
are of the form xP
+ xH for
some solution xH
of the homogeneous system Ax = 0.
|
|
: A(xP
+ xH)
= AxP
+ AxH
= b + 0
= b, so xP
+ xH
is a solution of Ax = b.
|
|
: Let x
be any solution of Ax = b
and define y = x
– xP.
Then Ay = Ax
– AxP
= b – b
= 0, so y
is a solution of Ax = 0
and x = xP
+ y. For xH
= y, x
is of the form xP
+ xH for
some solution xH
of the homogeneous system Ax = 0.
|
You can see how this works our when you solve a linear system and its corresponding
homogeneous system together. Suppose for example you solve both systems
|
x1
+ 2x2 + x3
+ x4 |
= 3
|
2x1
+ 5x2 – x3
+ 3x4
|
= 5
|
|
|
|
x1
+ 2x2 + x3
+ x4 |
= 0
|
2x1
+ 5x2 – x3
+ 3x4
|
= 0
|
|
Their augmented matrices are |
|
|
|
which reduce to |
|
|
|
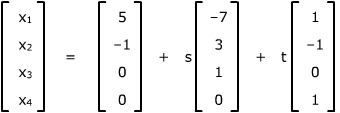
Their solutions are then |
| x1 = |
5 – 7s + t |
| x2 = |
–1 + 3s – 1 |
| x3 = |
s |
| x4
= |
t |
|
|
| x1 = |
–7s + t |
| x2 = |
3s – 1 |
| x3 = |
s |
| x4
= |
t |
|
or in column matrix form, |
|
|
|
Notice what happens: the parameter part of the solution of the non-homogeneous
system is the solution to the homogeneous system, and the remaining part is
the particular solution you get by putting s = t = 0.
Now suppose we have a square homogeneous
linear system.
If A is a square matrix, then the
homogeneous linear system Ax
= 0 has only
the trivial solution if and only if A
is invertible.
|
|
: If A
is invertible and x is any solution of
Ax =
0, then (multiply by A–1)
AA–1x
= A–10,
i.e. x = 0
- there is only the trivial solution.
|
Assume that A
is not invertible; then its reduced row echelon form R
is not the identity and so has a row of zeroes at the bottom. The reduced
row-echelon form of the augmented matrix [A|0]
is [R|0],
so it also has a row of zeroes at the bottom, and thus fewer leading 1's
than rows. Since A and R
are square, [R|0]
has fewer leading 1's than columns left of the bar, so its solution contains
parameters. The system thus has a non-trivial solution.
|