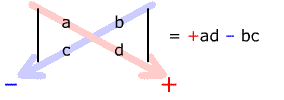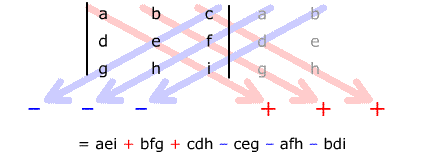The formal definition of a determinant

The determinant of a square matrix is built out of "signed elementary products" of the numbers in that matrix. Let's look at elementary products first.

An elementary product of a n x n matrix is the product of n numbers from the matrix with no two of them in the same row or the same column.

An n x n matrix has n! elementary products. Here's an example for n = 4.

Each elementary product has an associated sign which depends on the rows and columns its numbers come from. The sign can be determined as follows.

Write down a list of the matrix entries in the elementary product.
Write down a list of the numbers of the rows these entries appear in, in the same order as the list of entries.
Write down a list of the numbers of the columns these entries appear in, in the same order as the list of entries.
By repeatedly swapping pairs of numbers in the list of column numbers, transform that list into the list of row numbers, and count the number of swaps you need.
The sign is positive if you need an even number of swaps and negative if you need an odd number of swaps. (The actual number of swaps you do or the order in which you do them turns out not to matter.)

Once we have the signed elementary products, we can define a determinant.

To find the determinant of a matrix

calculate all its signed elementary products

add up the results.

Notation for the determinant of A: either det(A) or |A| (i.e. replace the brackets by bars)

Needless to say, calculating a determinant by using the definition would consume a horrendous amount of time even for quite small matrices. In practice, we don't use the definition to calculate determinants, but we do use it to prove rules that help us calculate determinants more efficiently.

There are two special cases for which it's relatively easy calculate to determinants using elementary products: when the matrix is 2 x 2 or 3 x 3. For both, you can find the correct signed elementary products by a type of "down-right is +, down-left is – " rule. Here's how that works.

For a 2 x 2 determinant, the elementary product on the down-right diagonal has a + sign attached, and the elementary product on the down-left diagonal has a – sign attached.

		For a 3 x 3 determinant, write ghosts of the first two columns on the right. The elementary products along the down-right diagonals are assigned plus signs and the ones along the down-left diagonals are assigned minus signs.

These rules give simple shortcuts for small determinants that are definitely worth learning. But the rule does not work for larger matrices – it doesn't even give all the elementary products, let alone their correct signs. Look at the 4 x 4 example above, and note that only 8 of the 24 elementary products lie on a down-right or down-left diagonal.

There's one elementary product for which the sign is always easy to determine, for any size matrix.

For a square matrix of any size, the sign attached to the elementary product of the numbers down the main diagonal is always +.

Proof: The numbers on the main diagonal have the same row number as column number, so zero swaps are necessary to transform the list of row numbers into the list of column numbers. Since 0 is an even number, the sign is +.