Adjoints and inverses

To find the inverse of a matrix using cofactors, you first need to know what its adjoint is.

The adjoint of a square matrix A is the matrix formed by

replacing every entry of A by its cofactor

taking the transpose of the result.

Notation for the adjoint: adj(A)

The basic property of adjoints.

For any square matrix A, Aadj(A) = det(A)I.

Proof: The entry in row i and column j of Aadj(A) is the product of row i of A and column j of adj(A). The entries of column j of adj(A) are the cofactors of row j of A.

If i = j, we have the product of row i of A and the column of cofactors of row i, which is just the expansion of det(A) along row i.

If i ≠ j, we have the product of row i of A and a column of cofactors from a different row of A. This is the same as expanding a determinant with two equal rows (row i is repeated inside the cofactors), and so is 0.

The complete product has det(A) along the main diagonal and zeroes elsewhere, and so is det(A)I.

If in addition A is invertible, then A–1 = adj(A)/det(A).

Proof: This relation follows from the first by dividing by det(A):
A{adj(A)/det(A)} = I.

So:

To find the inverse of a matrix using cofactors

Find the determinant (must not be 0 for an inverse to exist).

Find the adjoint.

Divide the adjoint by the determinant to get the inverse.

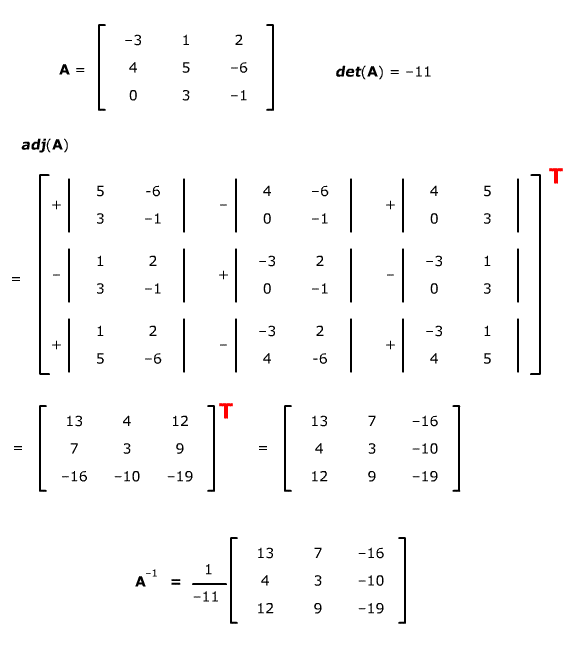
An example.

(The T for transpose is big and red as a reminder, in case you got absorbed in finding the cofactors and forgot to take the transpose at the end.)