Laplace expansion of determinants

The most important use of cofactors is to calculate large determinants recursively, that is, to express a determinant in terms of smaller determinants, which can in turn be written in terms of smaller determinants, which in turn ... – all the way down to 2 x 2 determinants, which are then easy to calculate.

To expand a determinant along a row or column

Find the cofactors of every number in that row of column.

Multiply each number in the row or column by its cofactor.

Add up the results.

The expansion is sometimes called the Laplace expansion of the determinant.

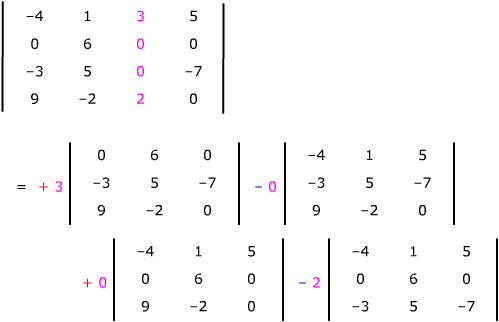
Here's an example. The determinant is expanded along its third column.

Things to notice about this example.

The alternating signs. These are actually the cofactor signs, taken from the checkerboard pattern. You figure out what the first one is, and then just alternate signs along the row or column.
This expansion exchanges the work of evaluating a single 4 x 4 determinant for the work of evaluating four 3 x 3 determinants. But for this particular example, two of the numbers in column three are 0's, so it doesn't matter what their cofactors are, you need only evaluate two 3 x 3 determinants. It would have been even easier if we'd expanded along row two instead, which has three 0's – then you'd only have to bother with one 3 x 3 determinant in the expansion.

Cofactor expansion of determinants is very powerful when combined with row and column operations, especially for big determinants. If you can use row and column operations to get a row or column that is all zeroes except for one number, you can expand along that row or column and end up with a single determinant one size smaller to evaluate.

Here's an example. Suppose you want to evaluate the determinant

.

You notice that column three looks much like twice column 2, so you use the column operation C3 ← C3 – 2C2, which doesn't change the determinant.

.

You've got three zeroes in column three with only one column operation. The row operation R2 ← R2 – 3R5 will get you a fourth zero in column three.

.

Now expand along column three:

= – .

You've now got a single 4 x 4 determinant to calculate. Notice the two zeroes in the last column. One more row operation will get you another zero in that column: R3 ← R3 – R4.

– .

Expand along the last column.

– {–0(whatever) + 0(whatever) – 0(whatever) + (1)}

= – .

Evaluate this one by the diagonals method:

– {3 + 12 + 12 – (–9) – 8 – (–6)} = –34.