Coordinate systems and components in 3-space
Rectangular coordinate systems in 3-space are defined like rectangular coordinate
systems in 2-space, but with an extra axis.
| To define a rectangular coordinate system
in 3-space |
| Choose a point O
(the origin) and three
mutually perpendicular lines through O (the x
axis, y-axis
and z-axis). |
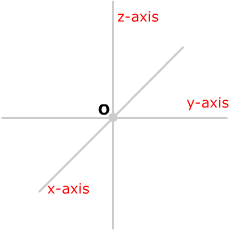 |
|
Choose a unit for measuring distances and a positive
direction along each axis. Assign each point on the axis its signed
distance from the origin as a coordinate.
|
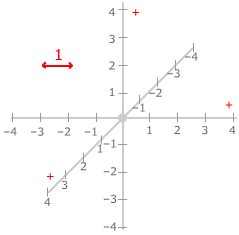 |
|
The axes also define three coordinate planes:
|
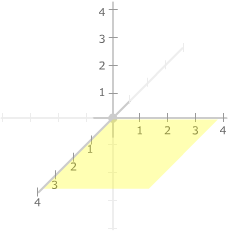 |
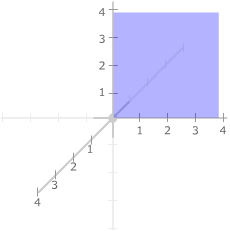 |
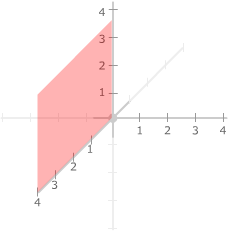 |
the xy-plane
containing the x-axis and y axis
|
the yz-plane containing
y-axis and z-axis
|
the xz-plane containing
the x-axis and z-axis.
|
|
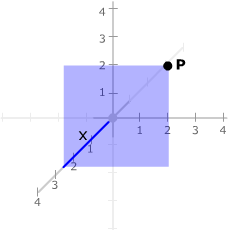
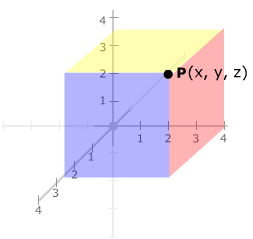
The x-coordinate
of a point P is the coordinate
x of the point on the x-axis where that axis meets the plane through
P parallel the yz-plane.
|
 |
|
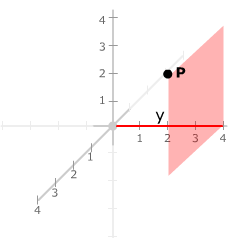
The y-coordinate
of a point P is the coordinate
y of the point on the y-axis where that axis meets the plane through
P parallel the xz-plane.
|
 |
|
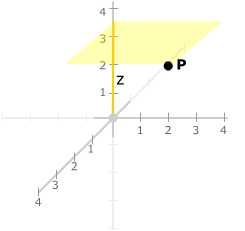
The z-coordinate
of a point P is the coordinate
z of the point on the z-axis where that axis meets the plane through
P parallel the xy-plane.
|
 |
|
The point P
is then represented by the ordered triple (x, y, z).
We write the point as P(x, y,
z).
|
 |
|
. To avoid making our picture
overly complicated, we usually draw only the positive parts of the axes unless
the negative parts are essential to the current situation. Also, note that we
usually draw the x-axis pointing "out" of the plane of the page, the
y-axis horizontally and the z-axis vertically. There are other orientations
(six orientations in total) which are sometimes used: here are the positive
axes of each.

Rectangular coordinate systems in 3-space are either right-handed
or left-handed. A system is right-handed
if, when you curl the fingers of your right hand so as to push the positive
x-axis onto the positive y-axis through 90°, you thumb points roughly in
the direction of the z-axis. The system is left-handed otherwise (or if you
do the same test with your left hand). The usual way of orienting the axes mentioned
before is right-handed (the first system in the picture above). Can you decide
whether the remaining five are right-handed or left-handed?
To define components for vectors in 3-space, we do essentially what we did
in 2-space: represent the vector by an arrow with its tail at the origin and
look at the coordinates of its head.
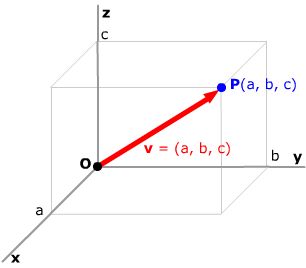
| Components of a vector in 3-space |
Given a rectangular coordinate system in 3-space
with origin O, represent each vector
by an arrow with its tail at the origin. Its head will then lie
at some point P(a, b, c). The vector
can then be represented by the ordered triple of numbers (a, b,
c). The number a is called the x-component
of the vector, the number b is called the y-component
of the vector and the number c is called the z-component
of the vector.
|
 |
|
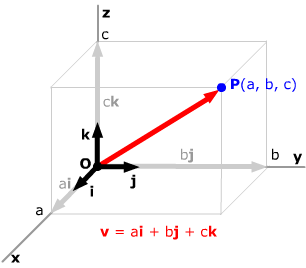
As before, we can write a vector in an alternate form using
the vectors
i = (1, 0, 0), j
= (0, 1, 0) and k = (0,
0, 1)
along the coordinate axes. In this form, any vector v
= (a, b, c) can be written as v = ai
+ bj + ck. |
 |
To calculate with components, we do essentially as we did in 2-space, but with
one extra component.
| Calculations with components in
3-space |
Suppose u,
v and w
are vectors in 3-space and c is any scalar. In terms of components with
respect to some coordinate system in 3-space, |
| If u
= (u1, u2,
u3 ), v
= (v1, v2,
v3) and w
= (w1, w2,
w3), then |
If u
= u1i
+ u2j
+ u3k,
v = v1i
+ v2j
+ v3k and
w = w1i
+ w2j
+w3k,
then |
u + v
= (u1 + v1,
u2 + v2,
u3 +
v3)
|
u + v
= (u1 + v1)i
+ (u2 + v2)j
+ (u3 + v3)k
|
cu = (cu1,
cu2, cu3)
|
cu = cu1i
+ cu2j
+ cu3k
|
–v = (–v1,
–v2, –v3)
|
–v = –v1i
– v2j
– v3k
|
u – v
= (u1 – v1,
u2 – v2,
u3 –
v3)
|
u – v
= (u1 – v1)i
+ (u2 – v2)j
+ (u3 – v3)k
|
0 = (0, 0, 0)
|
0 = 0i
+ 0j + 0k
|
| To prove these rules,
use the second component form for the vectors and the list of ten essential
rules. |
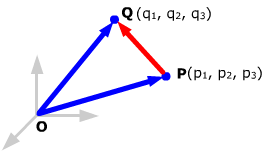
To find the components of the vector joining two points, proceed as you did
for 2-space.
The components of the vector PQ
from point P(p1,
p2, p3)
to point Q(q1,
q2, q3)
are
PQ
= (q1 – p1,
q2 – p2,
q3 - p3). |
 |
|
:
PQ = OQ
– OP = (q1,
q1, q3)
– (p1, p2,
p3) = (q1
– p1, q2
– p2, q3
– p3). |












