Vector geometry

The basic idea: represent vector quantities by arrows. More specifically, represent the size of the quantity by the length of the arrow and its direction by the direction of the arrow. Represent the velocity of an object moving 4 km/sec west by an arrow of length 4 pointing left, for example.
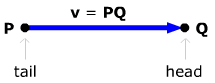
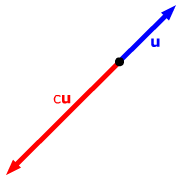
If a vector starts at point P (its tail) and ends at point Q (its head), we'll denote it by PQ, or else just by a single bold lower case letter like u or v.

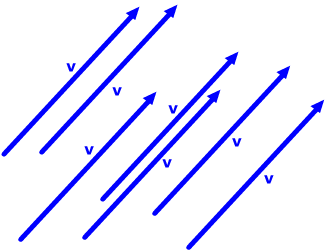
An arrow should represent only the size and direction of the quantity; it doesn't matter just where its head and tail are drawn as long as it has the appropriate length and direction. In particular, arrows with the same length and same direction are considered to be equivalent representations of the same vector. (This is useful when it comes to solving problems; you can draw your arrow wherever in your diagram works best.)

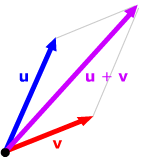
There are two ways to add vectors: the parallelogram rule and the "head-to-tail" or triangle rule.

Vector addition

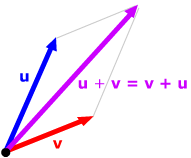
Parallelogram rule: Represent both vectors by arrows with the same tail. Form a parallelogram with the vectors as adjacent sides; then their sum has their common tail as its tail point and the fourth vertex of the parallelogram as its head.

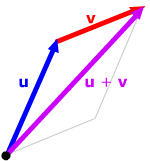
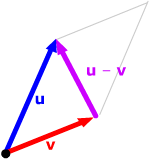
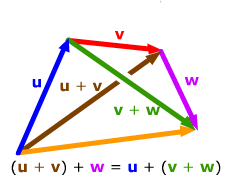
Triangle rule. Represent the second vector by an arrow with its tail at the head of the first vector. Their sum will have the same tail as the first vector and the same head as the second.

The two rules give the same sum, since the triangle of the second form is just half the parallelogram of the first form.

Using these rules over and over, it's possible to add many vectors together. If your vectors represented displacements on a computer screen, for example, such a sum could represent the final displacement of an object that moved 400 pixels down, 300 pixels left, and 500 pixels up.

It's possible that you end up back where you started; in that case the displacement is represented by a point.

The zero vector 0 is a vector with length 0, and is represented by a single point. Its direction can be assumed to be any direction that makes sense for the problem under consideration.

You'd get a zero vector by adding to one vector a vector of the same length but the opposite direction, for example.

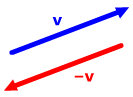
The negative of a vector v is the vector –v with the same length as v but in the diametrically opposite direction.

v + (–v) = 0.

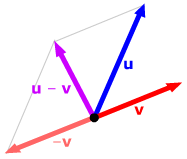
To subtract one vector from another, add its negative :

u – v = u + (–v).

Alternately, the difference of two vectors is the vector whose tail is the head of the second and whose head is the head of the first. (The parallelogram is congruent to the one above.)

Vectors can also be "scaled", or multiplied by scalars.

Scalar multiplication

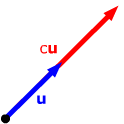
Suppose u is a vector and c is a scalar.

If c = 0 or u = 0, then cu is the zero vector.

If c > 0 and u ≠ 0, then cu is the vector in the same direction as u with a length c times the length of u.

If c < 0 and u ≠ 0, then cu is the vector in the direction diametrically opposite that of u and with length (–c) times the length of u.

Geometric vectors obey the same list of ten essential rules we had for matrices.

Ten Essential Rules for Geometric Vectors

Closure rules:
for geometric vectors u and v and any scalar c,

u + v is a geometric vector

cu is a geometric vector

Arithmetic rules for addition:
for any geometric vectors u, v and w,

u + v = v + u

u + (v + w) = (u + v) + w

There is a vector 0 such that u + 0 = 0 + u = u for all geometric vectors u.

For each geometric vector u, there is a geometric vector –u such that u + (–u) = 0.

Arithmetic rules for scalar multiplication:
for any geometric vectors u and v and any scalars c and d,

c(u + v) = cu + cv

(c + d)u = cu + du

(cd)u = c(du)

1u = u

Some of these rules are obvious from the definitions.

For example, the commutative rule u + v = v + u is clear from the parallelogram method of addition, since it doesn't matter which of the two vectors you write first.

The associative rule u + (v + w) = (u + v) + w for addition follows from the head-to-tail method of addition, since the result of either side is just a vector with the tail of the first vector and the head of the last.

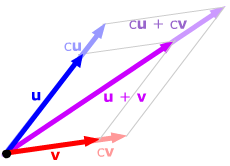
Other rules can be proved using basic geometry; for example, the distributive rule c(u + v) = cu + cv can be proved using similar triangles. (For c > 0 as in the diagram, prove that cu + cv is parallel to u + v and has length c times the length of u + v.)

For the other distributive rule, (c + d)u = cu + du, compare the lengths of cu, du and (c + d)u for c and d with all possible signs.