Areas and volumes

The area of the parallelogram in 3-space with sides u and v is
|u x v| .

The area of the triangle in 3-space with sides u and v is
(1/2) |u x v| .

Proof: The area of the parallelogram is its base times its height. Its base is |u|, its height is |v|sin θ, so its area is |u||v|sin θ = |u x v| .

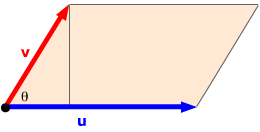The area of the triangle is half that of the parallelogram, or (1/2)|u x v|.

 

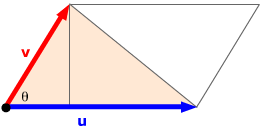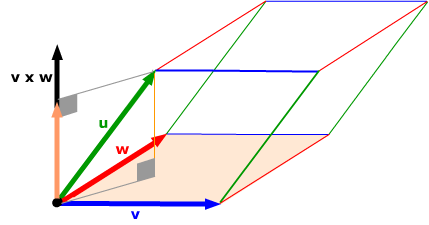
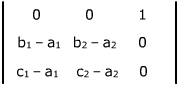
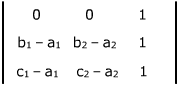To calculate volumes, we use a combined dot and cross product.

The triple product, or box product, of the vectors u, v and w in 3-space is the scalar u•(v x w).

Coordinate form: if u = (u1, u2, u3), v = (v1, v2, v3) and w = (w1, w2, w3), then the triple product is the determinant

The second form follows by expanding the determinant along row 1: you get the components of u in row 1 times the cofactors formed from rows 2 and 3, which are the components of v x w.

 

A parallelepiped is a "sheared brick", i.e. a solid whose faces are all parallel parallelograms.

 

 

The volume of a parallelepiped with adjacent edges u, v and w is |u•(v x w)|.
Proof: The volume is the area of the base times the height.

The area of the base is |v x w|.

Since v x w is perpendicular to the base (it's perpendicular to both v and w), the height is the length of the projection of u onto v x w, or

The coloured piece is a scalar, and can be brought outside the norm if you put absolute value signs around it:

The bottom of this scalar is positive, so this becomes

or

The volume of the parallelepiped is thus the product of this height with |v x w|, or |u•(v x w)|.

 

A useful formula that has applications in 2D computer graphics.

The area of the triangle in 2-space with vertices (a1, a2), (b1, b2) and (c1, c2) is

Proof: Consider 2-space to be the xy-plane in 3-space. The area you want is the area of the triangle with vertices A(a1, a2, 0), B(b1, b2, 0) and C(c1, c2, 0).

Calculate: AB = (b1 – a1, b2 – a1, 0) and AC = (c1 – a1, c2 – a2, 0).

Now calculate (1/2)|k•(AB x AC)| two different ways.

Since AB x AC is parallel to k,

(1/2)|k•(AB x AC)|

= (1/2)|k||AB x AC| |cos θ|       where θ is 0 or π
= (1/2)|AB x AC|      since |k| = 1 and since cos θ = ±1
= the area of triangle ABC.

But the triple product k•(AB x AC) is equal to

Apply the row operations R2 ← R2 + R1 and R3 ← R3 + R1:

k•(AB x AC) = .

Now apply the column operations C1 ← C1 + a1C3 and C2 ← C2 + a2C3 to get

k•(AB x AC) = .

The area of the triangle is then (1/2)|k•(AB x AC)| = .