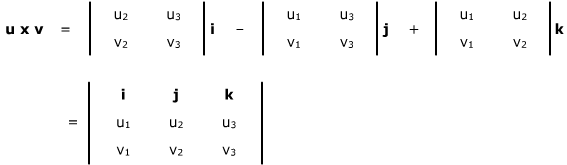
Cross products

The cross product of two vectors is defined only for vectors in 3-space, and is another vector.

Cross products have many properties that make them ideal for certain geometric applications.

Calculation rules for cross products

For any vectors u, v and w in 3-space and any scalar c,

u x 0 = 0,    0 x u = 0   and   u x u = 0

u x v = –(v x u)     (cross products are anti-symmetric)

u x (v + w) = u x v + u x w   and    (u + v) x w = u x w + v x w    (distributive rules)

c(u x v) = (cu) x v = u x (cv)

i x j = k,    j x k = i,     k x i = j    (note the cyclic i → j → k → i order in each)

|u x v| = |u||v|sin θ, where θ is the angle between u and v

u x v is orthogonal to both u and v, and (provided the coordinate system is right-handed), u, v and u x v form a right-handed system of vectors.

Proofs: Most of these rules can be proved by the "brute force" method: write the vectors in component form, then calculate out the left-hand side, calculate out the right-hand side and show they are equal.

For the "length" property |u x v| = |u||v|sin θ, first use brute force to prove the Lagrange identity (u x v)•(u x v) = (u•u)(v•v) – (u•v)2 then substitute (u x v)•(u x v) = |u x v|2,  u•u = |u|2,  v•v = |v|2  and  u•v = |u||v|cos θ to get |u x v|2 = |u|2|v|2 – |u|2|v|2cos2θ = |u|2|v|2 {1 – cos2θ} = |u|2|v|2 sin2θ. Take positive square roots to get |u x v| = |u||v|sin θ.   (sin θ ≥ 0 since 0 ≤ θ ≤ π)

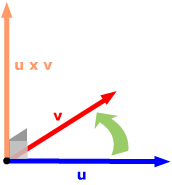
The other rules are straightforward, except for the last one. It's easy to show by brute force that u x v is orthogonal to u and v, but it's not easy to show that they form a right-handed system. (This means that, if you curve the fingers of your right hand so as to push u onto v through an angle of less than π, your thumb will point in the appropriate direction for u x v.) It's important to note that the original coordinate system must be right-handed as well for this to be true.

Notice one multiplication rule that's not included in this list: cross products are not associative. Here's a counterexample (an example that shows that something isn't always true). Calculate:

(i x i) x j = 0 x j = 0,

but

i x (i x j) = i x k = –j

so   

(i x i) x j ≠ i x (i x j) .

As we did when we defined dot products, we cheated a bit by using a coordinate system to define cross products. The last two rules on the list save us this time by giving us a coordinate-free description of cross products: the cross product of two non-zero vectors u and v is the unique vector that:

• has length |u||v|sin θ, where θ is the angle between u and v
• is perpendicular to both u and v
• has a direction given by the right-hand rule.

Since this description gives us both a unique length and a unique direction for the cross product, it determines the cross product uniquely, and without using coordinates.