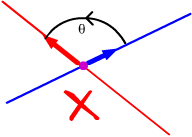
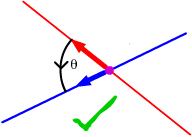
Angle between two lines. You can find the angle between two intersecting lines by finding the angle between their direction vectors. However, since the direction vectors for any line can have either of two directions, there are two possible results for the angle between the lines. The two angles sum to π, so for definiteness, we choose the smaller of the two (so the angle between two lines is always less than or equal to π/2). |
 |
 |
Example. These two lines intersect at (–1, 4, –3). What is the angle between them?
|
|
x = –1 + 2 t |
x = –1 – s |
The direction vectors for the lines are d = (2, 1, 1) and e = (–1, –2, 1). Then |d| = |e| = 61/2 and d•e = –3, so the cosine of the angle between the direction vectors is –3/6 = –1/2. It follows that the angle between the direction vectors is 2π/3. This is greater than π/2, so the angle between the lines is π– 2π/3 = π/3.
Angle between two planes. The angle between two planes is the smallest angle between a pair of lines one in each plane. It turns out to be the smaller angle between the planes looked at "edge on". Looked at edge on, the planes appear as lines and their normals as vectors perpendicular to these lines. Since the normals are perpendicular to their planes, a little geometry shows that the angle between the planes is the same as the angle between their normals or π minus this angle, whichever is smaller. |
 |
Example. Find the angle between the planes 2x + y – 2z = 3 and 3x + 3y = 4.
The normals to the planes are n = 2i + j – 2k and m = 3i + 3j . Then |n| = 3, |m| = 3.21/2 and n•m = 9. The cosine of the angle between these vectors is thus 1/21/2, so the angle between the planes is π/4.
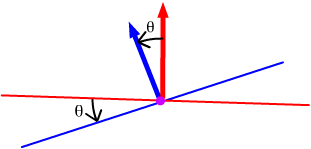
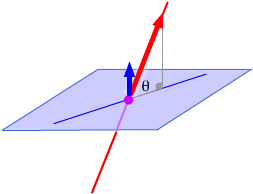
Angle between a line and a plane. The angle between a line and a plane is the smallest possible angle between that line and any line in the plane. The line in the plane that gives this angle is the one "directly under" the given line. To find the angle between the given line and the line in the plane, first find the angle between the line and a normal vector to the plane and subtract it from π/2. |
 |
Example. Find the angle between the plane x + y + 2z = 7 and the line x = 4, y = –2 + t, z = 5 + t.
The normal vector to the plane is n = i + j + 2k and the direction vector of the line is d = j + k. Then the cosine of the angle between these vectors is 3/(61/221/2) = 31/2/2, so this angle is π/6. The angle between the line and the plane is then π/2 – π/6 = π/3.