Distance from a point to a plane. Suppose we have a plane and a point not on it. The distance from the point to the plane is its distance from the plane along a line parallel to the normal vector to the plane.
The distance between two points is just the norm of the vector joining them.
The distance between a point and a line or a plane can be found using projections.
Distance from a point to a plane. Suppose we have a plane and a point not on it. The distance from the point to the plane is its distance from the plane along a line parallel to the normal vector to the plane.
|
 |
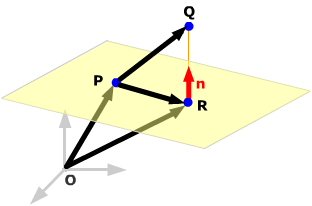
Example. Given the point Q(15, 3, 0) and the plane through P(5, 0, –5) with normal vector n = 3i + 4k, find
Draw a sketch. The distance you want is the length of the projection of PQ onto the normal vector, and the point on plane closest to Q is R. |
 |
Calculate:
PQ = 10i + 3j + 5k, projn(PQ) = 6i + 8k, so the distance from Q to the plane is |projn(PQ)| = 10.
The position vector of R is OR = OP + PR. Since PR is the component of PQ perpendicular to n, PR = PQ – projn(PQ) = 4i + 3j – 3k, so OR = (5i – 5k) + (4i + 3j – 3k) = 9i + 3j –8k. Then R is the point R(9, 3, –8).
Distance from a point to a line. The distance from a point to a line is the distance from that point to the closest point on the line, and is measured along a line perpendicular to the given line. |
 |
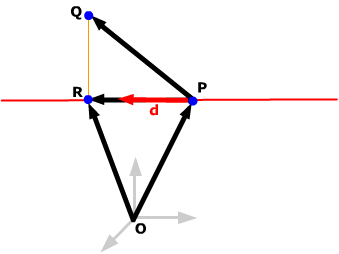
Example. Given the point Q(0, 4, 6) and the line (x, y, z) = (3 + t, –4 – 3t, – t), find
Draw a sketch. (P is a point on the line and d is its directon vector.) The distance you want is the length of the component of PQ perpendicular to d. The point on the line closest to Q is R. |
 |
Calculate:
The line has direction vector d = i – 3j – k and goes through point P(3, –4, 0).
PQ = –3i + 8j + 6k.
projd(PQ) = –3i + 9j + 3k, so the component of PQ perpendicular to d is PQ – projd(PQ) = –j + 3k. The length of this vector is 101/2, the required distance.
The position vector of the point R is OR = OP + projd(PQ) = 5j + 3k, so R is the point R(0, 5, 3).