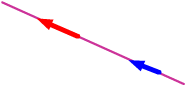
The lines coincide.
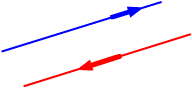
The lines are parallel.
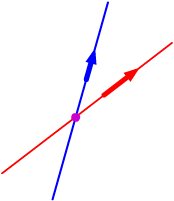
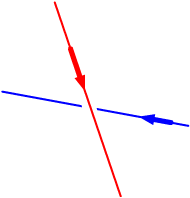
The lines intersect.
The lines are skew.
Intersections of two lines. In 2-space, there are three possiblities for the intersection of a given pair of lines: they either coincide, are parallel or intersect in a point.
In three-space, there are four possibilities.
 |
 |
The lines coincide.
|
The lines are parallel. |
 |
 |
The lines intersect. |
The lines are skew. |
You decide which case you have by looking at the direction vectors of the lines and then trying to find the point of intersection.
Example. Are the lines
|
|
x = 1 + t |
x = –2 – 2s |
coincident, parallel, intersecting or skew?
Their direction vectors are i + 5k and –2i + j which are not parallel, so the lines must be intersecting or skew. To see if they intersect, try to find a point of intersection. Any point (x, y, z) on both lines must satisfy all three of the equations
|
1 + t |
= x = |
–2– 2s |
From the last equation, t = –2 and from the second equation s = –3. But these values of s and t don't satisfy the first equation, so this system has no solution. There is no point of intersection, so the lines are skew.
Intersection of two planes. Two planes can intersect or not in three different ways.
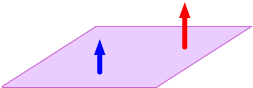 |
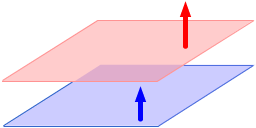 |
|
The planes coincide. |
The planes are parallel.
|
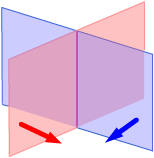 |
|
The planes intersect in a line. |
|
Example. Find any intersection of the planes
x + 2y + 2z = 0
x + 3y + 5z = –2
Their normal vectors are i + 2j + 2k and i + 3j + 5k, which are not parallel, so the planes intersect in a line. To find the line, solve the linear system of the two plane equations. The reduced row-echelon form of the augmented matrix is
so the solution is
x = –4 + 4t, y = –2– 3t, z = t.
We thus have the line through the point (–4, –2, 0) with direction vector 4i – 3j + k.
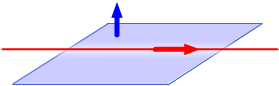
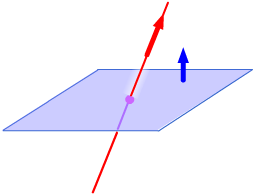
Intersection of a line and a plane. A line and a plane can intersect or not in three ways.
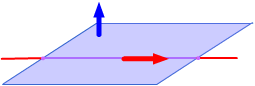 |
 |
The line lies in the plane.
|
The line is parallel to the plane.
|
 |
|
The line intersects the plane in a point.
|
|
Example. Where, if anywhere, does the line through P(0, 2, –2) with direction vector i – 3k intersect the plane 3x – 4y – z = 6?
The normal to the plane is 3i – 4j + k. Since (3i – 4j – k)•(i – 3k) = 6 ≠ 0, the line is not parallel to the plane or contained in it. To find the point of intersection,
Then t = 2, so the line intersects the plane at the point (2, 2, –8).