Lines

To describe a line, you need two pieces of information: a point on the line and a direction for the line.

The point can be specified as usual by its coordinates or its position vector r0, and the direction by a non-zero direction vector d.

Neither of these is unique; you can choose any point on the line and any direction vector parallel to the line (all direction vectors will thus be scalar multiples of each other).

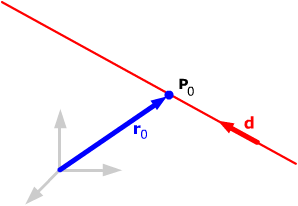Now, suppose r is the position vector of a generic point on the lline. The vector r – r0 is parallel to d, so for some scalar t, r – r0 = td, i.e. r = r0 + td.

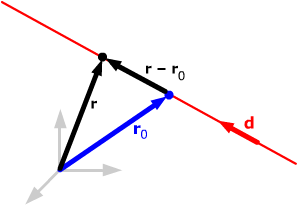The vector equation for a line through the point with position vector r0 and with direction vector d is

r = r0 +td

where t is a parameter ranging over all real numbers.

Now let's be more specific and use coordinates. Suppose that

the point has coordinates (x0, y0, z0), so its position vector is r0 = x0i + y0j + z0k
the direction vector is d = ai + bj + ck.

For a generic point r = xi + yj + zk on the line, we get

xi + yj + zk

= (x0i + y0j + z0k) + t(ai + bj + ck)
= (x0 +ta)i + (y0 + tb)j + (z0 + tc)k.

Set the i-, j- and k-components on each side equal to each other to get another way of representing the line.

The parametric equations for a line through the point P(x0, y0, z0) with direction vector d = ai + bj + ck are

x = x0 + ta
y = y0 + tb
z = z0 + tc

where t is a parameter ranging over all real numbers.

Given the parametric equations of a line, you should be able to read off a point on that line and a direction vector for the line. For example, if you're given the line

x = 2 – 3t
y = 3 + 4t
z = –1 + 5t

you should recognize immediately that the line goes through the point (2, 3, –1) and has a direction vector –3i + 4j + 5k.

For most problems involving lines, you will not be given a direction vector and point directly; you'll usually be given information that can be used to find them.

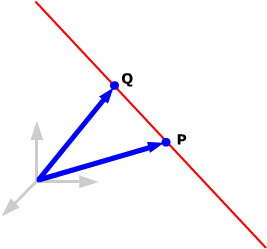
Example: Find parametric equations for the line through the points P(1, –2, 3) and Q(4, 0, –3).

Draw a sketch (always!). To find a line, you need both a point and a direction vector. You have two points to choose from, but you need to find a direction vector.

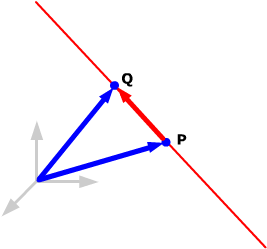
From the sketch you can see that the vector PQ lies along the line and so can be used as a direction vector. Calculate: PQ = 3i + 2j –6k, so using P for the point, the line has parametric equations:

x = 1+ 3t
y = –2 + 2t
z = 3 – 6t