Planes

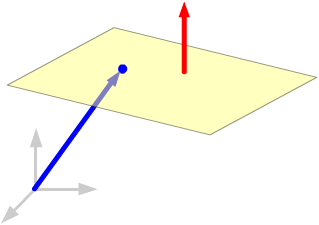
A plane in 3-space can be described by a point on it and a normal vector – a vector perpendicular to it. Any plane contains many points and has many normal vectors, all paralled to each other.

 

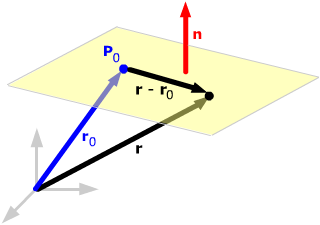
Suppose a plane has a normal vector n and passes through a point P0 with position vector r0. If r is the position vector of a generic point on the plane, then r - r0 lies in the plane and so is perpendicular to the normal vector: (r - r0)•n = 0.

 

The vector equation of a plane through the point with position vector r0 and perpendicular to the normal vector n is

(r –r0)•n = 0.

 

Now let's look at this equation in terms of components. Suppose that

For a generic point with position vector r = xi + yj + zk on the plane, we get

r – r0 = (x – x0)i + (y – y0)j + (z – z0)k,

so (taking the dot product with n)

a(x – x0) + b(y – y0) + c(z – z0) = 0.

The point-normal equation of the plane through the point P(x0, y0, z0) with normal vector n = ai + bj + ck is

a(x – x0) + b(y – y0) + c(z – z0) = 0.

 

Now multiply out the point-normal equation of a plane and put all the non-variable terms on the right

ax + by + cz = ax0 + by0 + cz0,

or equivalently (if we set d equal to the constant ax0 + by0 + cz0)

ax + by + cz = d,

a linear equation in x, y and z. It's possible to show that any equation of this form is the equation of some plane with normal vector ai + bj + ck.

Any plane with normal vector ai + bj + ck has an equation of the form

ax + by + cz = d

for some constant d, and any equation of this form is the equation of some plane with normal vector ai + bj + ck.

This equation of a plane is called its general equation, or standard equation.

You should be be able to read a normal vector of a plane directly from its general equation. For example, the plane with equation 5x – 7y + 4z = 3 has a normal vector 5i – 7j + 4k.

 

To find the equation of a plane, you need two pieces of information: a point on the plane and a normal vector for the plane. As with lines, you will not always be given each explicitly, but will be asked to find a point and a normal from other information.

 

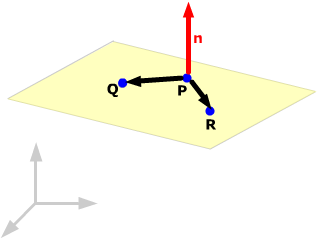
Example. Find the general equation of the plane through the points P(1, 2, 3), Q(2, 5, –1) and R(1, 4, 2).

To help you think, sketch a picture of the situation.

You need a point and a normal vector. You have three points to choose from, so you just need to find a normal vector.

 

The normal vector will be perpendicular to all vectors in the plane. You have three points in the plane, so you can find several vectors in the plane joining those points. If you take the cross product of any two of those vectors, you will get a vector perpendicular to the plane.

Find the vectors:   PQ = (1, 3, –4),   PR = (0, 2, –1).

Find their cross product: PQ x PR = (5, 1, 2).

Using P as the point, the plane then has point-normal form

5(x – 1) + 1(y – 2) + 2(z – 3) = 0.

Multiply out and simplify: 5x + y + 2z = 13.

 

Example. Find the standard equation for the plane containing the line r =( i + 2j + k) +t(2i - k) and the point P(2, 0, -2).

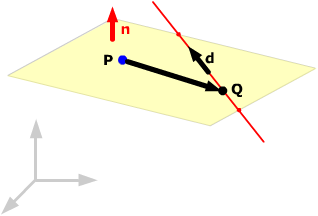
Draw a picture. You have two points to choose from: P(2, 0, –2) and the point on the line Q(1, 2, 1). You need to find a normal vector.

 

The normal vector must be perpendicular to the direction vector of the line, d = (2, 0, –1) and also perpendicular to the vector joining P and Q, which is PQ = (–1, 2, 3).

You can find a normal as before by taking the cross product of these vectors: d x PQ = (2, –7, 4).

Using P as the point, the plane has equation

2(x – 2) –7(y – 0) + 4(z + 2) = 0,

or    2x – 7y + 4z = –4.