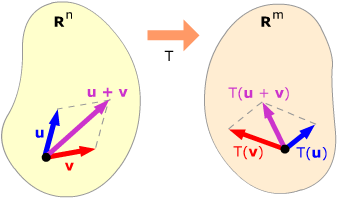
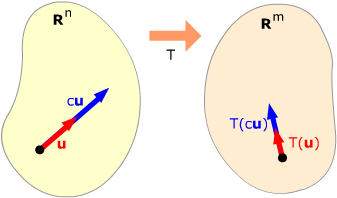
A linear transformation from Rn to Rm is a function T:Rn → Rm which preserves sums and scalar multiples. Specifically, for all vectors u and v in Rm and all scalars c:
T(u + v) = T(u) + T(v)
(The transform of a sum of two vectors in Rn is the sum of their transformed vectors in Rm.)
T(cu) = cT(u)
(The transform of a scalar multiple of a vector in Rn is that same scalar multiple of the transformed vector in Rm.)