A function f:A → B is one-one if no two elements of its domain A map into the same element of its codomain B.
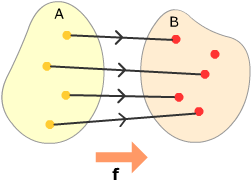
This function is one-one. No two • s map onto the same •.
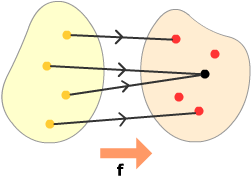
This function is not one-one, since two •s map onto •.
More function review: what does it mean for a function to be one-one (or one-to-one)?
A function f:A → B is one-one if no two elements of its domain A map into the same element of its codomain B. |
||
|
This function is one-one. No two • s map onto the same •. |
This function is not one-one, since two •s map onto •. |
|
Whether or not a linear transformation is one-one depends on its kernel.
|
The kernel of a linear transformation T:Rn → Rm is the set of vectors in Rn which transform into the zero vector in Rm.
|
|
Proof: If T is one-one, it can't map a non-zero vector into 0, since it already maps 0 into 0. This means that its kernel can contain only 0. |
| Suppose the kernel contains just the zero vector. To check if T is one-one, check if it can map two different vectors u and v in Rn into the same vector in Rm. If T(u) = T(v), then T(u – v) = T(u) – T(v) = 0. This means that the non-zero vector u – v is in the kernel of T, which is impossible since we assumed the kernel contained just 0. Then T cannot map different vectors into the same vector, and must be one-one. |
|
|
Proof: Suppose T has standard matrix A. Since T is one-one, its kernel contains only the vector 0. That means that the matrix equation Ax = 0 has only the trivial solution x = 0. The reduced row echelon form of A must then have leading 1's in each of its n columns, and thus must have n non-zero rows. It has m rows in total, so m ≥ n. |