A function f:A → B is onto if every element in its codomain B has some element of its domain A mapping onto it.
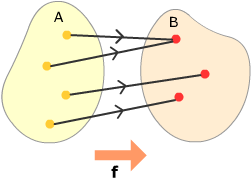
This function is onto, since every • has an • mapping onto it.
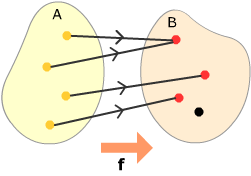
This function is not onto, since no • maps into •.
More function review: what does it mean for a function to be onto?
A function f:A → B is onto if every element in its codomain B has some element of its domain A mapping onto it. |
||
|
This function is onto, since every • has an • mapping onto it. |
This function is not onto, since no • maps into •. |
|
Whether or not a linear transformation is onto can be expressed in terms of its range.
| The range, or image of a linear transformation T:Rn → Rm is the set of vectors in its codomain Rm which are transforms of some vector in its domain Rn.
|
|
|
|
Proof: Suppose T has standard matrix A. Since T is onto, its range is all of Rm, so the matrix equations Ax = b has a solution for all b in Rm. Suppose m > n; then we'll find a b for which Ax = b has no solution. There are elementary matrices E1, E2, ..., Ek such that Ek...E2E1A = R, where R is the reduced row-echelon form of A. Define C = Ek...E2E1; then C is invertible and CA = R. Define b = C–1[0, 0, ..., 0 1]T. Now, if Ax = b, then CAx = Cb, so Rx = [0, 0, ..., 0, 1]T. But R has more rows than columns, and thus more rows than leading 1's. It must thus have a row of zeros at the bottom, so Rx must have a zero at the bottom. It doesn't, so our assumption that m > n must be impossible, and m ≤ n. |