Derek Powazek makes some interesting points about weblogs in a Mindjack interview, particularly about how they relate to journalism. I especially liked the last point: there's a major distinction between "real" personal weblogs and online community sites like Kuro5hin and Slashdot. I think there's another useful distinction: that between personal weblogs and "newsblogs" - those weblogs whose main raison d'être is to assemble current material from other websites or blogs, with varying degrees of personal comment. I considered doing that when I started this blog, but decided not to: I don't feel qualified to comment intelligently on most of the things I read, so I try to stick to topics I've thought about more than superficially.

Newsblogs can sometimes be "false advertising": merely citing a large number of timely articles tends to endow the writer with a cachet of knowledge and authority he or she may not deserve. I regularly scan one blog whose author keeps his posting rate high by reading cursorily but commenting opinionatedly, often along the lines of "this is what I've been saying all along". He's considered a knowledgeable guru in his field, and may well be, but his blog hasn't convinced me of that.

Back from CMESG2002, and have more or less recovered from too much eating and too little exercise and sleep. A curious thing I've noticed, from this and other education conferences: education people like to dance. Most conferences have some sort of associated social event in addition to the banquet or whatever; at most of the education conferences I've attended in the last few years, it's been a dance. Our mixture of math and ed folk was originally to have a river cruise and theatre outing (the latter was cancelled due to the lead's laryngitis). The riverboat had live music; spontaneous dancing ensued.

I've been to too many math conferences to count, and only one ever included dancing - usually it's been some sort of scenic/historical outing or a cultural event. So I'm curious: is this indeed a pattern common to education academics, and do other groups have other preferred social activities when they meet at conferences?

I'm at the CMESG2002 Conference (Canadian Mathematics Education Study Group). Like every conference, a mixed bag of the interesting and the not so interesting. A few highlights thus far:

* A tag-team plenary by Deborah Ball and Hyman Bass on the content knowledge necessary for teaching mathematics - not necessarily the same knowledge required by a practising mathematician. Echoes of Liping Ma's "profound understanding of elementary mathematics", but raised more questions about how to use that understanding - how do you design a question to test comprehension of ordering decimals, for example?

* A second plenary by Jon Borwein on The Experimental Mathematician: The Pleasure of Discovery and the Role of Proof. A nugget-rich presentation philosophical as well as mathematical and computational, and not easy to summarize, so I won't. Just one thing I've never really understood, even after a several-year association with Jon's lab: if "proof and rigour should be in the service of things worth proving", what is the worth of determining ever more and more digits of pi?

* A working group run by Nick Jackiw and David Pimm on Mathematics, the Written and the Drawn. On the relationships and contrasts between mathematical knowledge in symbolic/verbal form vs that in pictorial/diagrammatic form. Some interesting exercises, e.g. on the diffiiculty of communicating diagrammatic information verbally, and on eliciting symbolic/verbal information from dynamic geometry sketches. An insight into my personal learning style: my geometric intuition was severely curtailed when someone else was operating the mouse, even though we were cooperating verbally on the task. Score one for tactile learning, but what does this say about collaborative learning?

More to come in the next day and a half.

A statement by Darren Grem doubting the possibility or effiacy of non-linear argument makes Mark Bernstein take issue:

I'm completely happy with Mark's description of how our brains work non-linearly; mine certainly doesn't go in anything near logical, linear directions. But communication and argument is between brains, which is another story. To get an argument from my brain to yours, our respective brains have to encode and decode the words. No matter how non-linearly I structure those words, you still encounter them linearly in time, so I can't ignore that fact in the structuring. I ran into this problem once when trying to design a calculus course non-linearly - there were way too many concepts logically dependent on others to allow more than a few easy pathways through the material. My own perspective of calculus is certainly more associative than linear, but I'd expect my students to build that perspective gradually for themselves from linearly presented material, not absorb it directly from me. The non-linearity is in individual brains, not in the communication between them. (At least, not in the textual communication between them - multimedia is a whole 'nother ball game.)

For scientific arguments, at least (as opposed to rhetorical ones), I'm inclined to agree with Donald Norman (in The Design of Everyday Things):

A major caveat here: I haven't read the works Mark mentions nor many hypertexts, so I may be spouting off from ignorance here - there may well be well-developed techniques and tools for making non-linear arguments that I'm unaware of. If so, I'd like to see them - I could take another crack at that calculus course. I'm skeptical, though, certainly for areas as hierarchical as mathematics. I'd like to see an example of a non-linear argument of any sort - say a blog post, done in a pop-up, perhaps, to allow multiple threads/pages. I suspect that, even if it does work, it'll still be less clear and longer than a regular post. The shortest distance from one point to another, in rhetoric as well as mathematics, is still a straight line.

As a research mathematician, I'm not likely ever to become famous, though I've had a reasonably successful career. The thing I'm most likely to be remembered for (if only because my name has become attached to it) is a circle I discovered a few years back.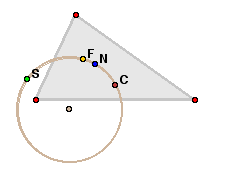

The discovery was that, for any triangle with no two sides equal, four special points - its circumcentre, nine-point centre, first Fermat point and second Fermat point - are all on a circle, and always in that order. There's always a circle through any three points not on a line; a circle through four special points is a rarity.

If you're interested in triangle geometry and would like to know more, I've put up a website with interactive applets and explanations of what the points are and how the circle was discovered.

Montessori schools use self-correcting materials to teach children basic concepts - for example, to teach about size, a series of graduated cylinders each fitting into a corresponding hole in a wooden bar. If the child makes an error by putting a cylinder into the wrong hole, there'll be a cylinder left over at the end that fits nowhere, so the child knows there's been an error. The point: discovery of the error comes from the nature of the task, not from a teacher or a test.

I've been thinking about how to apply this principle online. There are obvious advantages: errors encountered in the immediate context of the learning are more likely to be understood than those not, for example. The feedback is non-authoritive and less intimidating than correction from a teacher (less math anxiety!). Materials designed to provide self-correcting feedback need fewer self-tests or other forms of formative assessment inserted into the learning, a resource savings.

Some forms of learning are already self-correcting to some extent - programming, for example - if the program is incorrect, it just won't run. Most forms of experiential learning (learning by doing) can be designed to work this way - try it, see what works, what doesn't, and revise/re-do accordingly. Designing online learning experiences that include self-correction clearly needs a deep understanding of the subject matter and how people learn it. Where do we go from there?

"Booklend is the creation of a man with a postage meter, a roomful of books, and an urge to share. Borrowing a book is free, and you're welcome to keep the book until you're done. Read it at your leisure -- nobody likes to be rushed while they're reading. When you're done, pop it back in the mail. We'll even pay return postage. "

A delightful anachronism in an age of instant, online everything.

The photo was taken in 1901, aboard the SS Sardinian. The two gentlemen left and right are Messers George Kemp and Percy Paget, assistants to the man in the middle, Guglielmo Marconi. They're on their way from England to St. John's, Newfoundland where they'll conduct an experiment that proves conclusively that radio signals can cross the Atlantic.

The lad in front is Stanley Green. He's probably unclear on the significance of what they're up to, but is nonetheless pleased to get his picture taken with important people. He and his family are immigrating to Newfoundland. His small sister Violet, later to become my grandmother, would recall very little of the trip or of the man Marconi when interviewed many years later by a local radio station. Except for one thing: "He kissed me!", she remembered.

Nanny lived a full and active life, and got to see radio, television and a man on the moon. She didn't get to see home computers or the internet, but I have no doubt that, were she alive today, she'd be writing a blog bragging about the family's early involvement in wireless. In the garden, on an iBook with an AirPort card.

Another article, this time in Syllabus Magazine, deprecates the value of content in online courses relative to other factors. And it may be correct.

It's correct if you accept its view of what content is: a "commodity", to be poured into a course much like water into a bucket ("shovelware", in the current parlance). It's correct if the medium of communication has no consequences for how content is communicated - if you can just port print to pixels and expect it to work as before. It's correct if you have no vision of what onscreen content could be, of how interactivity with the content could not only change how it is communicated, but change the actual "content of content".

The true value of online courses, claims the article (predictably), comes from the interpersonal interactions within a community of faculty and students, not to mention the accreditation of one's learning by a name university. In other words, it comes from replicating online those facets of the "university experience" deemed to be significant non-virtually. And currently, this may also be correct.

Long-term, things will change. Predictions:

* As we learn to design content rather than "pour" it, learning from online materials will become much easier than learning in a classroom with a teacher. The "grammars" of online content communication, interaction and simulation will become better understood, and the need for professorial interaction to learn content will diminish.

* Students of the future will satisfy their need for interpersonal interaction and community in authentic, life-context settings rather than at a university (online or otherwise). Most will be apprenticing or working while learning, and will belong to well-developed on- and off-line communities of work, learning or common interest.

* Assessment/accreditation will become separate from learning. Learners wanting only to learn will be able to do so online; those who need their learning evaluated will apply to professional testing centres (possibly run by universities, but not necessarily). An added bonus: a more objective assessment than an individual professor's final grade in a course he himself taught.

What will happen to universities? They may evolve into predominantly research organizations (many are already). They may become mentoring organizations rather than teaching ones, motivating students and helping them integrate their learning through multiple sources into a coherent whole (a little like the British "tutor" system). Much depends on if and how universities can "re-vision" themselves. In any case, they'll no longer hold a monopoly on content or its learning (and they're starting to feel the pinch already). And if they don't evolve? then, as Walter Stewart so aptly puts it, "they'll make great monuments".

Remember when the only way to send pictures in email was to convert them to ASCII images? Extremely coarse-grained, black and white, ... - the good old days? Don't fret; you can now do the same on a web page. TEXT-IMAGE.com will take your colour BMP, GIF, JPG or PNG and convert it into the modern equivalent: a coloured HTML text image.

Amazing what you can do with enough font tags. I have just one question: WHY? Why take an image already in a format any modern browser can display and convert it into HTML in order to display a crude form of it in a browser? The site guestbook is full of raves - am I missing something here?

"... This website consists of about 2500 pictures, each representing a single minute of the day in some shape or fashion. " Set the control panel and display it on your desktop. Server: A version of Apache reduced to a 25k text file and running on a Tandy. "We take our web hosting very seriously at humanclock.com, therefore we have installed 4 'AA' batteries in the webserver in case of power failure."

From Humanclock.com.

Each of the four cards below has a colour on one side (red or yellow) and a shape on the other (circle or square). Which of the cards must you definitely turn over to decide if the cards break the rule "if there's a circle on one side, then the other side is yellow"?

This test of logical reasoning and its variations are known as the Wason selection task (see the quiz "So you think you're logical?" on the Philosopher's Magazine site). As the quiz authors point out,

They record that only 13% of those doing this version of the quiz get it right. However, if the same logical problem is presented in the context of a "cheating scenario" (breaking a social rule), things change. When the problem is to determine if the rule "if someone drinks alcohol, he must be over 21 years old" is being broken, the success rate soars to 77%. A tentative explanation: "the human mind has evolved to detect violations of conditional rules, when these violations involve cheating on a social exchange."

Whatever the explanation, it's clear that, in everyday life, we don't normally use abstract logic to solve problems; we're highly influenced by contexts. How does this affect how we teach math?

First, it means that we start with those contexts, not logic. We build on students' existing instincts about size, shape, number, and present ideas concretely. School math has always done this (the "new math" aberration aside). University math tends to get into "rigour" rather quickly; the logical development of a topic often takes precedence over instinctive understanding, even in inherently applied subjects like calculus. (Texts like James Stewart's Concepts and Contexts are beginning to reverse this tendency.)

Eventually, however, we have to get beyond contexts to the logic. Especially for mathematics: abstracting ideas out of their contexts is the whole point of math. This point is lost on some proponents of "situated learning" type educational theories, who insist that every problem be an application to some real world situation (early editions of the Hughes-Hallet book Calculus took this approach). Understanding calculus logically and decontextualized is a necessary prerequisite for applying it to novel contexts, including further mathematics.

The appropriate learning path is from intuitive contexts to logical abstractions and then to applications of those abstractions to new contexts. As a trained mathematician, I had no difficulty applying the logic I learned long ago to the Wason task: turn over the red card and the one with the circle. To understand the logic behind my choice, see the quiz website.

Martin Dunwoody, a mathematician at Southampton University, is on his way to proving the Poincaré conjecture (maybe). The conjecture is one of the most famous unsolved problems in mathematics; a solution brings a million dollar prize and fame (in mathematical circles, at least).

What's so interesting about this, according to the Free Online Scholarship (FOS) newsletter, is how he's going about communicating his work. Rather than submitting a final polished manuscript to a journal, he's been submitting successive drafts to an open preprint server. Instead of receiving a few formal referee's reports months later, he's been getting immediate informal feedback from a highly interested community of peers, and using it to revise his work. The newsletter concludes:

What interests me more than publishing economics here is the new research paradigm: prototyping. The standard paradigm (submit only finished research for evaluation) has several drawbacks, chief among them the limited, delayed and often non-constructive feedback to the researcher. Prototyping (producing and distributing incomplete work for public evaluation and repeatedly revising it based on the feedback) looks to be a much faster and effective process: it supports the researcher's ongoing work rather than merely evaluating its final product.

There are drawbacks, of course, and questions to be resolved. A public evaluation of one's life obsession, however helpful, is not everyone's cup of tea. If the feedback from others is substantial, who deserves the credit? How credible is the evaluation process if everyone can have a say? What if the progress of one's academic career is predicated on formal, finished publications? There's no shortage of objections, nor of objectors, particularly among the vested interests in academic publishing (see the FOS newsletter).

Those of us who already prototype our ideas in blogs have seen the advantages and have fewer qualms.

If you're a puzzle fan like I am, you'll appreciate MazeWorks, a collection of computerized versions of some of the classics. The rules for most are deceptively simple; the solutions are quite another story.

As a mathematician, I suppose I should be interested in doing a thorough study of these things as an exercise and arriving at a rigorously thought out solution path. Actually, I just like mucking around with them. As I do with the four drawers crammed full of puzzles and games I've collected over the years - can't solve most of 'em; can't be bothered to analyse 'em - they're play, dammit, not work.

Puzzles and games are more fun on a computer than with their physical incarnations, though I'm not sure why; perhaps because they go faster. I do know I win more games on the computer - my solitaire win rate is amazing! I think it has something to do with short term memory. Physically moving things around is distracting as well as time consuming. Simple onscreen clicking allows longer sequences of likely moves to be implemented before they're forgotten. My theory, anyway.

On the other hand, there's something to be said for the look and feel of games and puzzles finely crafted from nicely grained wood. Which probably explains the visual appearance of the MazeWorks site.

"First it was by itself, probably the first home video game. I'm not really sure. Since then, countless varieties have been created. From Pong: The Movie to 3-D Pong. But none of them ever compared with the original.

Until now. Pong: The Text-Based Game, is about to take the world by storm. It has all the elements that people liked from the original and new elements that will cause Pong: The Text-Based Game to attract itself to an entirely new generation of players."

From Karber.net. Oooohh, the excitement! A simple but illustrative demonstration that what works successfully in one medium need not in another. Though it goes in the opposite direction, a caution for designers of onscreen educational content who seek to port print to screen.