The competition in the race is very strong and seconds count, so Fran decides to use calculus to find her turnoff point more exactly. She draws a diagram:
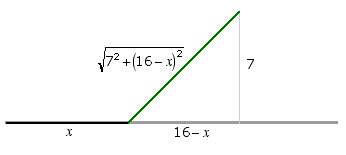
and then finds an expression for her total time for the ride in terms of the turnoff distance x.

The next step is to minimize the time, so she differentiates the function, using the chain rule on the second part:
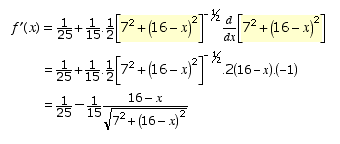
She sets the derivative equal to zero.
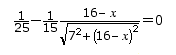
She notices that x always occurs as part of the chunk 16-x, so she solves first for 16-x:
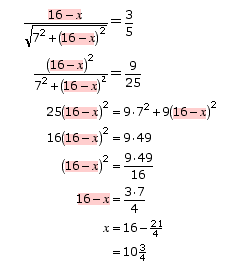
Does this answer agree with your estimate using the analyser?
8. Fran thinks it's common sense that her answer gives a minimum. Rebecca isn't so sure, so she decides to check the sign of the second derivative at x=10.75. She calculates
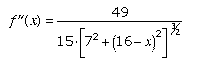
and realizes she doesn't need to substitute x=10.75 to be sure of a minimum. How does she know this?