| This definition is certanly non-intuitive, so we should first
check that it at least makes sense, i.e. that it always gives
a unique number that can be called the distance between the two
points.
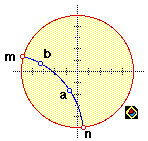
Notice that the cross ratio is real and positive, since  , ,  , ,  , and , and  are concyclic, with the pairs are concyclic, with the pairs  , ,  and and  , ,  not separating each other. This is important, since logarithms
are defined only for positive reals: the formula at least produces
a number. not separating each other. This is important, since logarithms
are defined only for positive reals: the formula at least produces
a number.
Is this number unambiguously defined? The only potential source of ambiguity is in the order
of the edgepoints. But switching the two just replaces the cross
ratio by its reciprocal and the logarithm by its negative: the
absolute value produces the same result either way, so there is
no ambiguity.
Something useful to note: if  and and  are chosen so that are chosen so that  , ,  , ,  , and , and  are in cyclic order (as in the sketch), the cross ratio is in
fact greater than are in cyclic order (as in the sketch), the cross ratio is in
fact greater than  (check it out) and logarithm is then positive. Thus for (check it out) and logarithm is then positive. Thus for  , ,  , ,  , and , and  in cyclic order, we may drop the absolute value in the distance
formula. in cyclic order, we may drop the absolute value in the distance
formula. |
 |

