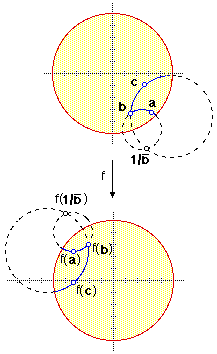
Any direct Poincaré motion  preserves the circles that contain the rays forming the sides
of an angle preserves the circles that contain the rays forming the sides
of an angle 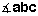 . The other point on both circles is . The other point on both circles is  , so its image , so its image 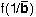 must be on both image circles. But both image circles also contain
the inverse of must be on both image circles. But both image circles also contain
the inverse of 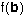 , i.e. , i.e. 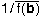 , so , so 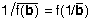 . Now, since . Now, since  preserves cross ratios, preserves cross ratios,
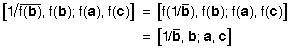
Take arguments of both sides; then 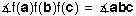 . .
|
 |
![]()
![]() .
.

