To introduce interactivity into Poincaré, I used Geometer’s Sketchpad (GSP). GSP is a highly interactive geometry software package designed mainly for grade school geometry. It allows students to construct geometric figures that can dragged or otherwise moved about – the students can interact with the geometry. Of course, the early version I used for Poincaré had fewer features than the current version – a single page per file, no graphing and no tables to mention a few. More importantly, however, it lacked JavaSketchpad, which allows current GSP sketches to be exported as applets and inserted into webpages.

However, browsers then had a very useful feature they don’t have now: they could use any application on the user’s computer as a “helper application”. Specifically, you could configure your browser to use the helper application to open a downloaded file of the appropriate type automatically. I used this functionality to allow users with Sketchpad (even its demo version) on their computers to download GSP sketches and immediately interact with them.

First, I told the users how to configure their browsers to make GSP a helper application for GSP sketches – a bit detailed, but not terribly complicated. Then, for each GSP sketch, I made a slightly smaller GIF of the initial appearance of that sketch, put a GSP “badge” on it to show that it represented a downloadable file, inserted the GIF into the appropriate place in its webpage, and linked it to the downloadable sketch. When the student clicked on the GIF, the effect was of a static diagram springing into life, ready for manipulation – or so I hoped.

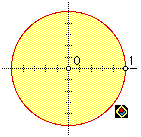
Here’s an example: this one is a picture of an “empty” Poincaré universe.

This picture is indeed live: if you click it, you browser will download it, and if you have a version of Geometer’s Sketchpad on your computer, you can open it and interact with it. (The demo version of GSP will allow you to interact but not to save.) This particular sketch could be used as a starting point for many investigations, so I made an icon for it that I could link to from any part of the project.

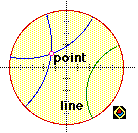
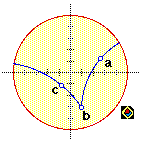
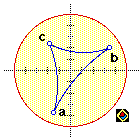
Other sketches in the project contained constructed points, lines and other objects. Here are a few live examples.

	Some lines in the Poincaré universe. Each can be moved by dragging one of the points that define the line.		Through any point not on a given line (green) there pass infinitely many lines (e.g. the blue ones ) not intersecting the first line.
	An angle in the Poincaré universe. It can be changed by dragging its vertex b or point a or c on its sides.		A draggable triangle in the Poincaré universe, used to investigate the triangle inequality.

The latest version of Sketchpad appears to have corrupted some carefully designed captions and labels I made for some of the original sketches – I’m not sure why.

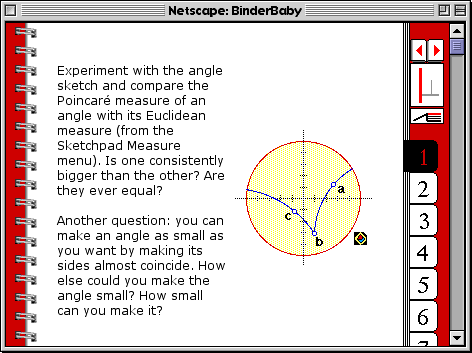
Here’s a screenshot of a typical page of the Poincaré project as it appeared in a BinderBaby notebook. The accompanying questions were intended to encourage students to experiment with the sketch and build an intuitive feel for Poincaré geometry.

Interacting with these sketches posed a few difficulties unavoidable with the technology used:

• the yellow background was unfortunately selectable, making it sometimes difficult to select individual objects on it
• points and other objects inside the circle-universe could be dragged inappropriately to positions outside the universe

All in all, though, the sketches worked essentially as I wanted them to. Given the limitations of the technology at the time, this method of using helper applications was (in my opinion, anyway) a rather clever way to introduce interactivity into online mathematics materials.