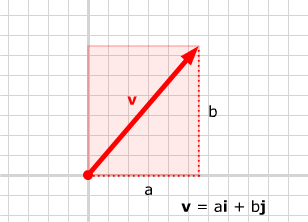
Calculating the length of a vector in 2-space in terms of its components is a direct application of the theorem of Pythagoras. Suppose
v = ai + bj .

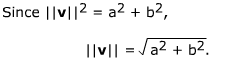
The length of a vector v is written as ||v||.

The length of a vector is also called the norm of the vector.

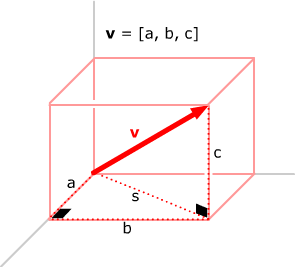
Calculating the length of a vector in 3-space in terms of its components is a double application of the theorem of Pythagoras. Suppose
v = ai + bj + ck.

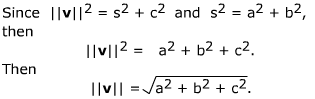
Rules for calculating with vector lengths

For any geometric vectors u and v and any scalar c,

• ||0|| = 0
• If u ≠ 0, then ||u|| > 0.
• ||cu|| = |c| ||u||
• ||u + v|| ≤ ||u||+||v||     (triangle inequality)

 

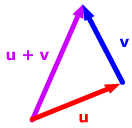
The first three rules are clear from the geometry of vectors and their components. The triangle inequality just says that the length of any side of a triangle is no greater than than the sum of the lengths of the other two sides - apply that observation to the triangle rule for addition of vectors.

Sometimes we need to use a vector to describe only a direction in 2-space or in 3-space, without worrying about the length of the vector. We can do this by always converting a vector in the appropriate direction to a "standardized" vector of length 1 pointing in the same direction. This is called normalizing the vector, and vectors of length 1 are called unit vectors.

Suppose we have a non-zero vector v in the appropriate direction. We need a unit vector in the same direction, i.e. we need to multiply v by a scalar so that the result has length 1. Since v has length ||v||, if we multiply v by the reciprocal of ||v||, the resulting vector will have length 1: the normalized vector is .

Thus:

To normalize any non-zero vector in 2-space or 3-space, multiply that vector by the reciprocal of its length.