In 3-space, when we used a standard basis {i, j, k} derived from a coordinate system, we talked about the components of a vector - for example, the components of the vector 2i - 4j + k are [2, -4, 1]. What happens if we use a different basis for 3-space? I.e., if {b1, b2, b3} is a basis of 3-space and v = 2b1 + 5b2 - 4b3, then can we say the components of v in this basis are [2, 5, -4]?

The answer is yes, but we have to clear up a few technical details first.

The first issue has to do with the order of the basis vectors. A basis was defined to be a certain type of set of vectors. Technically, the order of elements in a set is irrelevant, so the sets {i, j, k} and {i, k, j} are just different ways of writing the same basis. But then the vector
v = i + 3j +5k has different components with respect to the two sets: [1, 3, 5] with respect to {i, j, k} and [1, 5, 3] with respect to {i, k, j}.

If we want the component representation of vectors to be unambiguous, we need to assume (at least when talking about components) that all bases are in fact ordered sets of vectors - i.e. the order of the vectors in a basis matters, and bases with the same vectors but in different orders are in fact different bases.

The second issue also has to do with ambiguity: can a single vector have more than one component representation with respect to the same basis? The answer is no, but the situation is hard to visualize (at least in 3-space), so we'll prove it algebraically.

Suppose you have an ordered basis {b1, b2, b3} in 3-space, and suppose there were a vector v in 3-space with

v = p1b1 + p2b2 + p3b3

for one set of scalars p1, p2 and p3, and

v = q1b1 + q2b2 + q3b3

for another set of scalars q1, q2 and q3. Subtract the two equations:

0 = (p1 - q1)b1 +(p2 - q2)b1 +(p3 - q3)b3.

But {b1, b2, b3} is a basis, so the vectors b1, b2, b3 are linearly independent. This last equation is a linear dependence relation among
b1, b2 and b3, so its coefficients must all be 0:

p1 - q1 = 0,   p2 - q2 = 0,   p3 - q3 = 0.

Then  p1 = q1, p2 = q2, p3 = q3, so in fact, the two representations for v are really the same. The same argument works in 2-space, so in general, no vector can have more than one representation in terms of a given basis.

With these technicalities out of the way, we can define components with respect to a basis.

If B = {b1, b2} is an (ordered) basis of 2-space and v = c1b1 + c2b2 is any vector in 2-space, then the components of v with respect to B are defined to be

[v]B = [c1, c2].

If B = {b1, b2, b3} is an (ordered) basis of 3-space and
v = c1b1 + c2b2 + c3b3 is any vector in 3-space, then the components of v with respect to B are defined to be

[v]B = [c1, c2, c3].

You can use the components of vectors to find sums and scalar multiples just as you did when you used the standard basis E = {i, j} in 2-space or E = {i, j, k} in 3-space. For example, if vectors v and w in 2-space have components [v]B = [p, q] and [w]B = [r, s] with respect to the basis B = {b1, b2}, then

v = pb1 + qb2, w = rb1 = sb2

and

v + w = (p + r)b1 + (q + s)b2

i.e.

[v + w]B = [p + r, q + s].

The same sort of calculation works in 3-space, and for scalar multiples as well. In general: to find the components of the sum of two vectors, add their components pairwise. To find the components of a scalar multiple of a vector, multiply the components of that vector by the scalar.

Recall how the standard basis vectors i,and j are defined in 2-space: first a rectangular coordinate system is constructed; then the vectors i and j are defined to be the vectors with tail at the origin and head at the points (1, 0) and (0, 1) respectively. In other words, you start with a coordinate system and use it to define the standard basis vectors.

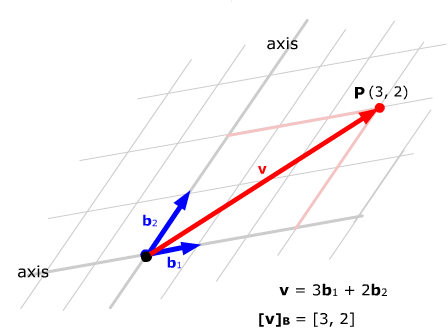
Now that we have different bases for 2-space, we can reverse this process and use the vectors of any basis to define a coordinate system. The idea: choose two lines through the origin along the basis vectors as coordinate axes. Use the basis vectors to define a unit coordinate along each axis. Optionally, set up a coordinate grid using lines parallel to the two axes. Then, to assign coordinates to any point in 2-space, look at the point's position vector and represent the point by the components of that vector in the new basis. Use those components as the coordinates of the point.

In the picture below, the point P has coordinates (3, 2) with respect to the coordinate system defined by the basis B = {b1, b2}.

It's important to understand that, when you represent a vector in a non-standard coordinate system, you are not changing the vector in any respect, just the coordinates which describe it. In the diagram below, you can see how one particular vector is represented in several different coordinate systems. Notice that, when you change the basis, the vector itself doesn't change, only the coordinate system "behind" it changes.

 

You can define coordinate systems from bases in 3-space in an exactly analogous manner: each basis vector defines an axis and a distance unit along that axis. Pairs of basis vectors span the coordinate planes. The coordinates of any point are defined to be the components of its position vector with respect to the given basis.