If we can use components with respect to different bases to represent vectors, can we use those components to do vector geometry just as we did with the standard basis components? Well, some geometry, yes, but not all of it.

You know that you can do sums and scalar multiples of vectors in general components just as you did in the standard components, so things like the vector equation of a line work fine in general components: with respect to a basis B, a line through r0 with direction vector d has vector equation

[r]B = [r0]B + t[d]B.

But there are problems when it comes to distances, lengths and angles or any formula depending on dot products. A simple example involving dot products: suppose b1 = i and b2 = i + j; then b1•b2 = 1 . But in the basis B = {b1, b2}, we have [b1]B = [1, 0] and [b2]B = [0, 1], and
[1, 0]•[0, 1] = 0, not 1.

Recall how the formula for the length of a vector is obtained: by using the theorem of Pythagoras on right angled triangles. These triangles were right angled because each of their sides was parallel to or perpendicular to a coordinate axis in a rectangular coordinate system - a coordinate system with perpendicular axes. Furthermore, each standard basis vector had length 1, so the lengths of the sides of these triangles was (up to sign) the same as the corresponding vector component.

If you use a more general basis to define a coordinate system, then

• the coordinate axes may not be perpendicular to each other
• the scale defined alone each axis need not corresponds to distance along that axis, and different scales may be used along each axis.

General coordinate systems can create havoc with dot product related component calculations - unless you choose your basis wisely.

The bases we need to use are orthonormal bases.

A basis B = {b1, b2} of 2-space is an orthogonal basis if its vectors are orthogonal, i.e. if b1•b2 = 0. The basis is an orthonormal basis if it is orthogonal and its vectors all have length 1, i.e. if

b1•b2 = 0

and

b1•b1 = 1, b2•b2 = 1.

 

A basis B = {b1, b2, b3} of 3-space is an orthogonal basis if its vectors are pairwise orthogonal, i.e. if b1•b2 = 0, b1•b3 = 0 and
b2•b3 = 0. The basis is an orthonormal basis if it is orthogonal and its vectors all have length 1, i.e. if

b1•b2 = 0,   b1•b3 = 0,   b2•b3 = 0

and

b1•b1 = 1,   b2•b2 = 1,   b3•b3 =1.

Calculating lengths, distances and angles in coordinates ultimately boils down to calculating dot products: for any vectors u and v in 2-space or 3-space,

• the length of u is given by ||u|| = (u•u)1/2
• the distance between the points with position vectors u and v is
  ||u - v||
• the angle between u and v is
          .

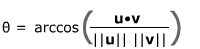Once we have a rectangular coordinate system (i.e. one based in an orthonormal basis), the dot product is calculated just as before. Let's look at dot products in 3-space to see why.

Suppose we have an orthonormal basis B = {b1, b2, b3} and two vectors v and w with

[v]B = [v1, v2, v3]   and   [w]B = [w1, w2, w3].

Then

v = v1b1 + v2b2 + v3b3   and   w = w1b1 + w2b2 + w3b3,

so

v•w = (v1b1 + v2b2 + v3b3)•(w1b1 + w2b2 + w3b3)
       = v1w1b1•b1 + v1w2b1•b2 + v1w3b1•b3 +
              + v2w1b2•b1 + v2w2b2•b2 + v2w3b2•b3 +
              + v3w1b3•b1 + v3w2b3•b2 + v3w3b3•b3
       = v1w1(1) + v1w2(0) + v1w3(0) +
              + v2w1(0)+ v2w2(1) + v2w3(0) +
              + v3w1(0)+ v3w2(0) + v3w3(1)
       = v1w1 + v2w2 + v3w3.

In other words, the usual formula for dot products works in any coordinate system built on an orthonormal basis. The calculation above works in 2-space as well; there's just no third component involved. It follows that, as long as you use an orthonormal basis, the usual component formulas for length, distance, angles and so on will work as before, since they can be written in terms of dot products.

Orthogonal bases are "almost" orthonormal in the sense that their vectors already go in appropriate directions, and just need to be normalized to have length 1. For example, the vectors 3i + 4j and 4i - 3j in 2-space are orthogonal, but have length 5. Multiply each by 1/5 to normalize them: the vectors

(3/5)i + (4/5)j    and    (4/5)i - (3/5)j

then form an orthonormal basis of 2-space.