There are two ways to define the dot product of two vectors.

• use the geometric properties of the vectors
• use the components of the vectors.

Suppose we start with two vectors u and v, both either in 2-space or in 3-space.

Geometric definition of a dot product

 

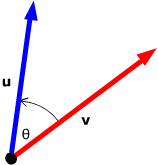
The dot product of u and v is defined to be the scalar

u•v = ||u|| ||v|| cos θ

where θ is the angle between the vectors. (θ is always taken to be between 0 and π inclusive.)

Coordinate definition of a dot product

For vectors with components u = [u1, u2] and v = [v1, v2] in 2-space,

u•v = u1u2 + u2v2.

For vectors with components u = [u1, u2, u3] and v = [v1, v2, v3] in 3-space,

u•v = u1v1 + u2v2 + u3v3.

These two definitions seem very different but actually amount to the same number; the second is just the first expressed in terms of components. To see how this works, we'll use the Law of Cosines for triangles:

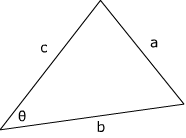
If a triangle has sides of lengths a, b and c and an angle θ between the latter two sides, then

a2 = b2 + c2 - 2bc cos θ.

 

 

Now let's apply this law to the triangle formed by u, v and their difference.

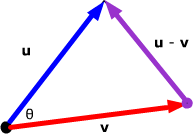We get

||u - v||2 = ||u||2 + ||v||2 - 2||u|| ||v|| cos θ.

Notice that the last term is almost the geometric form of the dot product. Let's solve for it in terms of the lengths of the vectors:

2||u|| ||v|| cos θ = ||u||2 + ||v||2 - ||u - v||2.

You already know how to calculate vector lengths in terms of components, so you can simplify the right-hand side. We'll do it for 2-space vectors; it works the same for 3-space vectors (just include the third component of each vector). Let u = [u1, u2] and v = [v1, v2] .

2||u|| ||v|| cos θ
     = (u12 + u22) + (v12 + v22) - {(u1 - v1)2 + (u2 - v2)2}
     = u12 + u22 + v12 + v22 - {u12 - 2u1v1 + u22 + v12 - 2v1v2+ v22}
     = 2u1v1 + 2v1v2

Divide by 2 to get ||u|| ||v|| cos θ = u1v1 + u2v2.

Why do we have two definitions of the dot product? The definitions are equivalent, of course, but each is more "natural" in certain contexts. If you're doing vector geometry, the geometric form is more natural, especially since it clearly doesn't depend on the coordinate system you're using, only on coordinate-independent geometric quantities (lengths and angles). The component form is easier to calculate with and is more useful algebraically, especially when it comes to generalizing dot products to vectors in "4-space" or "5-space" or "n-space". But as a first definition, it seems to depend on the coordinate system you are using - it's not immediately clear that you'd get the same dot product if you chose a different coordinate system.

In this diagram, you can compare the two definitions for different pairs of vectors. (change the vectors by dragging their heads).