The orthogonal projection of a vector onto a line can be thought of as the shadow of the vector in the line, produced by light beams perpendicular to the line. The diagram below shows the projection of a vector (blue) onto a line. Change the blue vector by dragging its shaft, its tail or its head. Notice that if you only reposition the blue vector (by dragging its shaft), its projection remains the same (but is perhaps repositioned). Which vectors project onto the zero vector? Which vectors project onto themselves?

Let's look for a formula for the orthogonal projection of a vector w onto a line. We have to specify the direction of the line somehow, so we'll assume there's a vector u which gives the direction of the line. The notation for the orthogonal projection of v onto u (i.e. onto the line determined by u) is proju(v). Move v so that its tail lies on the tail of u.

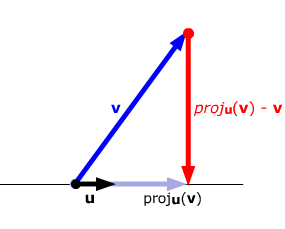
We know that proju(v) = au for some scalar a. Since proju(v) - v is orthogonal to u, we have that (au - v)•u = 0. Multiply out the dot product and solve for a: au•u - v•u = 0, so
a = v•u/u•u. Then

.

Since the vector u is only in the formula for proju(v) to describe the direction of the line, only its direction should play a part in this formula. Let's see what happens if we replace u by a scalar multiple w = cu. Then w•w = (cu)•(cu) = c2u•u and v•w = v•(cu) = c(v•u) , so

.

In other words, it doesn't matter whether we choose u or w to represent the direction of the projection; the result is the same projection vector.

Sometimes it is useful to be able to decompose a vector into the sum of two orthogonal vectors. For example, the force of gravity acting on an object sitting on an inclined plane can be decomposed into the sum of a force parallel to the plane and a force perpendicular to the plane. If the force along the plane is great enough to overcome friction, the object will slide down the plane.

 

 

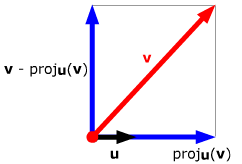In general, we want to be able to decompose a vector v into the sum of a vector in a specific direction (given by some vector u) and a vector orthogonal to u. From the picture to the right, it's clear that the vector in the direction of u is proju(v). Furthermore, since the two blue vectors must sum to v, the vector orthogonal to u is v - proju(v).

This vector v - proju(v) is called the component of w orthogonal to u. We thus have the orthogonal decomposition

v = proju(v) + {v - proju(v)}.

Sketch a rough copy of this diagram on paper and then sketch in the two vectors proju(v) and projv(u).