adj(A) is the matrix formed by
- replacing every entry of A by its cofactor
- taking the transpose of the result.
Proof: The entry in row i and column j of Aadj(A) is the product of row i of A and column j of adj(A). The entries of column j of adj(A) are the cofactors of row j of A, so (because of the transpose) the entry in row i and column j of the product Aadj(A) is the product of row i of A and the column of cofactors from row j of A.
If i = j, we have the product of row i of A and the column of cofactors of row i, which is just the expansion of det(A) along row i.
If i ≠ j, we have the product of row i of A and a column of cofactors from a different row of A. This is the same as expanding a determinant with two equal rows (row i is repeated inside the cofactors), and so is 0.
The complete product then has det(A) along the main diagonal and zeroes elsewhere, and so is det(A)I.
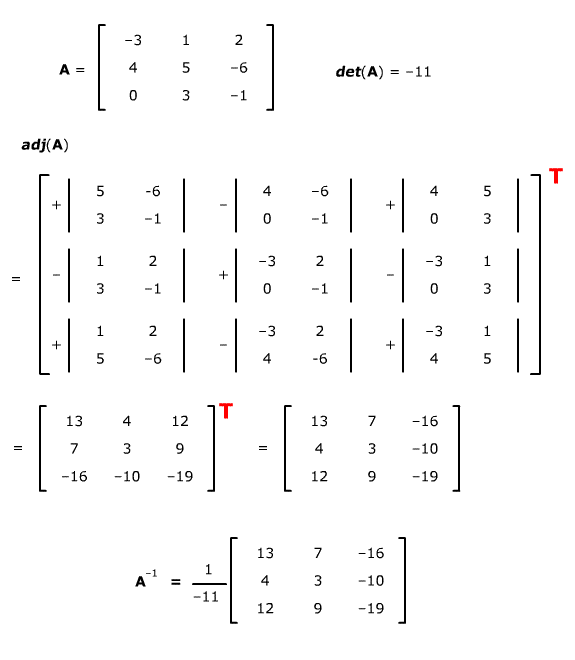 (The T for transpose is
big and red as a reminder, in case you got absorbed in finding the cofactors
and forgot to take the transpose at the end.)
(The T for transpose is
big and red as a reminder, in case you got absorbed in finding the cofactors
and forgot to take the transpose at the end.)
.
This equation says that the matrix inside the brackets is the inverse of A , i.e.
.
- Find the determinant of the matrix, and make sure it's not zero (else the inverse doesn't exist).
- Find the adjoint of the matrix
- Divide the adjoint by the determinant to get the inverse.
 Minors,
Cofactors and the Laplace Expansion of Determinants Minors,
Cofactors and the Laplace Expansion of Determinants |
|||
| Introduction | Minors and cofactors | The Laplace expansion of a determinant | Adjoints and inverses of matrices |