The most important use of cofactors is to calculate large determinants recursively. Using what is known as a Laplace expansion, you can express a determinant in terms of smaller determinants, which can in turn be expressed in terms of smaller determinants, which in turn ... all the way down to 2 x 2 determinants, which are then easy to calculate.

Here's the determinant of the previous page expanded along row 2.

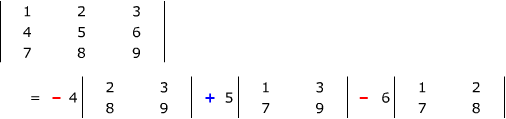
Note the signs: these signs actually belong to the cofactors of the numbers in the row you're expanding along, and are taken from the checkerboard pattern. You figure out what the first one is (it's the first sign in the row or column you're expanding along), and then just alternate signs along that row or column.

Here's a larger example: a 4x4 determinant you can expand along any row or column you choose. Note that there are two layers of information here: the expansion itself, and the highlighted details of that expansion.

 

Laplace expansions essentially exchange the work of evaluating a single large determinant for the work of evaluating multiple determinants one size smaller. Each cofactor gets multiplied by its corresponding row or column entry, so if that row or column entry is 0, you needn't evaluate the corresponding cofactor. The ideal tactic, then is to expand the determinant along the row or column containing the most zeroes.

A big determinant with only a few 0 entries could be a great deal of work to calculate directly with Laplace expansions. But if you know how to apply row and column operations to place zeroes in suitable positions, you can reduce the amount of work considerably.

Recall the elementary row and column operations and their effect on determinants.

Row operation	Column operation	Effect on a determinant
Ri ↔ Rj	Ci ↔ Cj	changes its sign
Ri ← cRi,   c ≠ 0	Ci ← cCi,   c ≠ 0	multiples it by c
Ri ← Ri – kRj, j ≠ i	Ci ← Ci – kCj, j ≠ i	has no effect

If you use row and column operations to replace all but one entry of a row or column of a determinant by zeroes, then, when you expand along that row or column, you reduce the work involved to evaluating a single determinant one size smaller. Look at the example which follows to see how to use this technique.

Suppose you want to evaluate the determinant

.

You notice that column three looks much like twice column two, so you use the column operation C3 ← C3 – 2C2, which doesn't change the value of the determinant.

.

You've got three zeroes in column three with only one column operation. The row operation R2 ← R2 – 3R5 will get you a fourth zero in column three and doesn't change the value of the determinant.

.

Now expand along column three:

+0(whatever) – 0(whatever) + 0(whatever) – 0(whatever)
                        + (–1)

=  – .

You've now got a single 4 x 4 determinant to calculate. Notice the two zeroes in the last column. One more row operation will get you another zero in that column: R3 ← R3 – R4. This row operation doesn't change the value of the determinant, so you get

– .

Expand along the last column.

– {–0(whatever) + 0(whatever) – 0(whatever)
                 + (1)}

= – .

You can evaluate this one by the diagonals method:

– {3 + 12 + 12 – (–9) – 8 – (–6)} = –34

To find the Laplace expansion of a determinant along a given row or column

• Find the cofactors of every number in that row or column
• Multiply each number in the row or column by its cofactor
• Add up the results.

It can be proved that, no matter which row or column you choose, you always get the determinant of the matrix as the result.

If you had to evaluate this determinant by Laplace expansions, which row or column would you choose for the first expansion, and why?