Large matrices are usually row reduced by computer software specially designed for the purpose. However, once you have a large matrix to row reduce, you have to consider how efficiently and accurately such software does the job.

Another computer issue: the accuracy of its calculations. Computers can only represent numbers, both input and calculated, as finite decimals, so any number must be rounded to the accuracy the computer and its software have available. Under certain circumstances, this rounding can produce wildly unpredictable results. Here's a simple example showing one possible problem.

Suppose the task is to row reduce the matrix

.

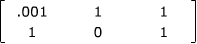(Note the small size of the entry .001 compared to the others.) If you calculate by hand, the exact reduced row-echelon form is

.

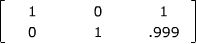Now suppose you have a (very inefficient) computer which can only represent numbers to two significant digits. (So for example, it rounds 1234 to 1200, .987 to .99 and 1.987 to 2.0.) You would expect your computer to produce the answer

,

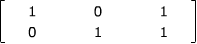since it rounds .999 to 1.

But the computer rounds numbers at every step of the row reduction calculations. Assuming it uses the standard Gauss-Jordan row reduction, it proceeds as follows (rounded numbers are highlighted).

Initial matrix:

.

This answer is badly off - if the matrix were the augmented matrix of a linear system in x and y, for example, you'd get the solution x = 0, y = 1 instead of the expected approximate solution x = 1, y = 1.

It's easy to construct similar examples for more sophisticated computers which can handle more significant digits - just change the .001 into something smaller - .0000000000000000000000001, perhaps. The solution to the problem is not to get a better computer, but to revise the Gauss-Jordan algorithm to avoid turning relatively small numbers into leading 1's. This is the basis of what is know as partial pivoting - modify the Gauss-Jordan row reduction algorithm by modifying the first step.

One way of measuring efficiency is to count the number of individual calculations the software has to do to row reduce a matrix of a given size - the additions and multiplications contributed by each row operation on all the entries in the row it affects. When you count all these calculations, it turns out that, for a computer, it is more efficient to reduce a matrix to row-echelon form first and then proceed to full reduced form. The first part (getting zeroes below the leading 1's) is sometimes called the "downward sweep", and the second part (getting zeroes above the leading 1's is then called the "upward sweep".

For a human doing the calculations by hand, there is the additional issue of how many times the matrix has to be written down during the calculation. In that case, it's probably more efficient to go directly to reduced form as described earlier, putting all the zeroes in each column with a leading 1 at once instead of in two steps.

The problem here is the number your computer turned into a leading 1 (i.e. .001) was relatively small - the computer had to multiply by a relatively large number (1000) to make that leading 1. That large number magnified the error in subsequent calculations, producing the inaccurate result.

Suppose the same computer first swapped rows to avoid this problem. The row reduction would proceed as follows.

Initial matrix:

Your computer now gives the expected approximate answer.

To reduce a matrix to reduced row-echelon form using partial pivoting

For each non-zero row in turn, from top to bottom:

1. Make sure the leading entry is not further right than any lower leading entry and that its absolute value is not smaller than any other leading entry in the same column below it. (Swap rows if necessary.)
2. Make the leading entry into a leading 1. (If necessary, divide the row by the leading entry.)
3. Make the other non-zero entries from the column with the leading 1 into zeroes. (Subtract multiples of the row with that leading 1 from those other rows.)
4. Move any zero rows you produced to the bottom. (Swap them with lower rows.)