Suppose we have three non-zero vectors (red, blue and yellow) in either 2-space or 3-space. Let's divide our exploration into three cases:

• all three are parallel
• at least two are not parallel, but all three lie in a plane
• no plane contains all three

 

 

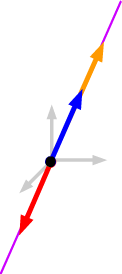
Case 1: all three vectors are parallel. Then the three vectors are all scalar multiples of each other, so any linear combination of them is also a scalar multiple of each. Their span must then consist of the vectors along the line through the origin containing the three vectors.

Case 2: at least two of the vectors are not parallel, but all three lie on some plane. (If the vectors are in 2-space, this plane is the whole of 2-space.)

The two non-parallel vectors span the plane containing them. The third vector is in this plane as well, so it is a linear combination of the first two. Then any linear combination of all three vectors is also a linear combination of the first two, so the span of all three is the same as the span of the first two, i.e. it is the set of all vectors in the plane.

 

 

Case 3: no plane contains all three vectors. (So the vectors are all 3-space vectors.)

 

 

 

 

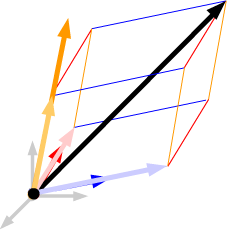
Recall how we expressed any vector in 2-space as a linear combination of two non-parallel vectors: by constructing a parallelogram with sides parallel to the two vectors.

In 3-space, with three vectors not all in the same plane, we can do something similar: given any generic vector in 3-space, we can construct the parallelepiped with edges parallel to the three given vectors and with the generic vector as diagonal. The parallelepiped determines three vectors parallel to the given vectors which sum to the generic vector. The span of these three vectors is thus all of 3-space.

The possibilities for the span of more than three vectors are the same as those for three vectors: all of 3-space, a set of vectors lying in a plane through the origin, a set of vectors lying on a line through the origin, or the set {0} (possible only as the span of the single vector 0). In general, you get the "smallest" of these which contains all the spanning vectors.

So, for example, 15 vectors which all lie in some plane through the origin in 3-space but not on a line through the origin will span that plane but cannot span all of 3-space. A set of 54 vectors in 3-space which don't all fit into some plane through the origin will span all of 3-space.