You can make the purple vector be any vector in 2-space and this will work, so the span of the red and blue vectors is all of 2-space.
Two non-parallel vectors in 2-space span the whole of 2-space. Two parallel vectors in 2-space span only the line of vectors containing them.
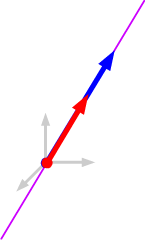
If the two vectors are parallel, then any linear combination of them must be parallel to both, so as before, the span of two parallel vectors consists of the line through the origin which contains the two vectors.
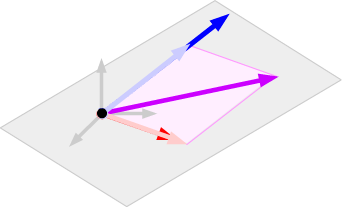 If the vectors are not parallel, then there is a single plane through the origin
containing them. Any linear combination of those vectors lies in that plane
and any vector in that plane is in their span (using the same sort of argument
we used for 2-space). So two non-parallel vectors in 3-space span the plane
of vectors containing them.
If the vectors are not parallel, then there is a single plane through the origin
containing them. Any linear combination of those vectors lies in that plane
and any vector in that plane is in their span (using the same sort of argument
we used for 2-space). So two non-parallel vectors in 3-space span the plane
of vectors containing them.
 Vector
Spans Vector
Spans |
|||
| Introduction | Definition of a span | The span of two vectors | The span of three or more vectors |