To choose a rectangular coordinate system in 3-space, you generalize what you did in 2-space.

In a rectangular 3-space coordinate system with origin O, represent each vector v by an arrow with its tail at the origin. Its head will then lie at some point P(a, b, c). We represent v by the ordered triple of numbers [a, b, c]. The number a is called the x-component of the vector, the number b is called the y-component of the vector and the number c is called the z-component of the vector.

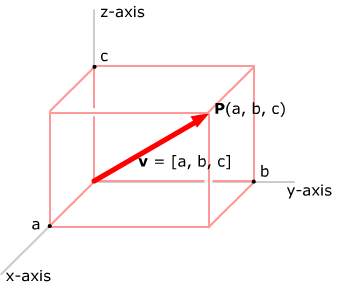
Note that the box with sides parallel to the coordinate planes and with point O and P at opposite corners has dimensions |a| in the x-direction, |b| in the y-direction and |c| in the z-direction.

As in 2-space, the position vector of a point stretches from the origin out to the point. In a rectangular coordinate system with origin O,

• The point P(a, b, c) has a position vector OP with components [a, b, c].
• A vector with components [a, b, c] is the position vector of the point P(a, b, c).

As in 2-space, the components of a vector joining two points can be found by subtracting the coordinates of those points (again in the order "head minus tail").

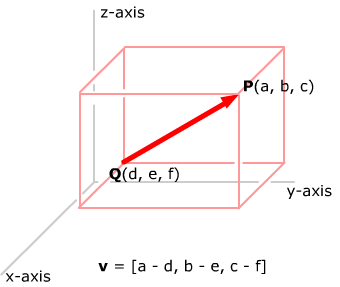
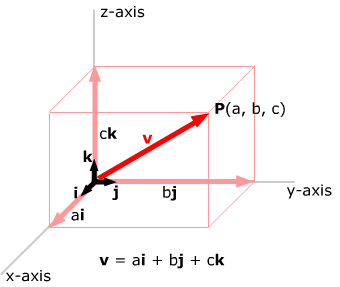
We can also represent vectors in component for without using brackets, as we did in 2-space. Define three vectors i = [1, 0, 0], j = [0, 1, 0] and k = [0, 0, 1]. The vectors each lie along a coordinate axis, and each has length 1. Any other vector v = [a, b, c] can then be written in the form v = ai + bj + ck.

Note that we usually draw the x-axis pointing "out" of the plane of the page, the y-axis horizontally and the z-axis vertically. There are other orientations (six orientations in total) which are sometimes used: here are the positive axes of each orientation.

Rectangular coordinate systems in 3-space are either right-handed or left-handed.

• Suppose you curl the fingers of your right hand so as to push the positive x-axis onto the positive y-axis through 90°. The coordinate system is right-handed if your thumb points roughly in the direction of the z-axis, and left-handed otherwise.
• Suppose you do the same test with your left hand. The coordinate system is then left-handed if your thumb points roughly in the direction of the z-axis and right-handed otherwise.

The usual way of orienting coordinate axes is right-handed (the first system in the picture above). Can you decide which of the remaining five are right-handed and which are left-handed?