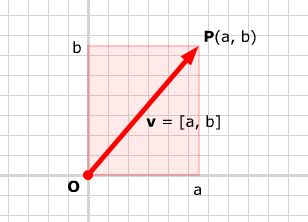
 In a rectangular 2-space coordinate system with origin O,
represent each vector v by an arrow with its
tail at the origin. Its head will then lie at some point P(a,
b). We represent v by the ordered pair of numbers [a,
b] (note the square brackets). The number a is called the x-component of
the vector, and the number b is called the y-component of
the vector.
In a rectangular 2-space coordinate system with origin O,
represent each vector v by an arrow with its
tail at the origin. Its head will then lie at some point P(a,
b). We represent v by the ordered pair of numbers [a,
b] (note the square brackets). The number a is called the x-component of
the vector, and the number b is called the y-component of
the vector.
Note that, when P is the first quadrant, a and b are the width and height of the box containing the vector, with sides parallel to the axes and points O and P at opposite corners. If P is in another quadrant, a or b may be negative, so in general, the box containing v has width |a| and height |b|.
For every point in the x-y plane, there is a vector starting at the origin and ending at that point. Call that vector the position vector of the point. Then
- The point P(a, b) has a position vector OP with components [a, b].
- A vector with components [a, b] is the position vector of the point
P(a, b).
A position vector gives the displacement of the point relative to the origin of the coordinate system you've chosen. Using position vectors is very useful when working with vector geometry - you can describe all the points on a line or plane, for example, by giving a formula for their position vectors.
Now change the vector by dragging its head or its tail. Make a vector starting at the origin and with either or both of its components negative; then drag it by its shaft again to see the effect on the head, tail and components.
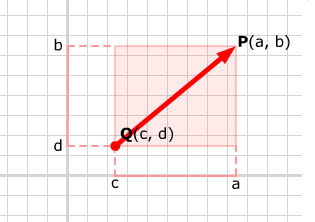
The general rule: the vector from the point Q(c, d) to the point P(a, b) has components PQ = [a - c, b - d].
Now suppose you have a vector represented by an arrow with its tail at some point (c, d) which is not the origin.
Its components are still given by the lengths of sides of the box containing it. In the picture, the box has width a - c and height b - d, so the vector QP has components [a - c, b - d] . (Note the order here: the components of the vector are give by the head coordinates minus the tail coordinates.)
This works no matter where the head and tail of the vector are located. In the diagram below, drag the vector by its shaft and notice the effect on its head, tail and components.
 The component representation of a vector is very
similar to the representation of a point; only the shape of the brackets
is different. (And many texts use round brackets for both.) There is another
way to represent vectors by their components which avoids this ambiguity.
The component representation of a vector is very
similar to the representation of a point; only the shape of the brackets
is different. (And many texts use round brackets for both.) There is another
way to represent vectors by their components which avoids this ambiguity.
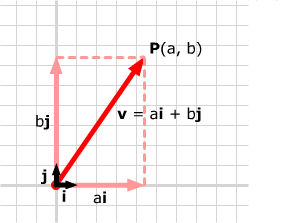
Define two special vectors i = [1, 0] and
j =
[0, 1]. These vectors both have length 1 and lie along the two coordinate
axes. Then any other vector v = [a, b] can be
written as a sum of scalar multiples of these vectors:
v =
ai + bj.
 Vectors
in Coordinate Systems Vectors
in Coordinate Systems |
||||
| Introduction | Two-dimensional coordinate systems | Three-dimensional coordinate systems | Using components to calculate with vectors | Calculating the length of a vector |