If u = [u1, u2] and v = [v1, v2], then
  • 0 = [0, 0]
  • –v = [ –v1, –v2]
  • u + v = [u1 + v1, u2 + v2]
  • u – v = [u1 – v1, u2 – v2]
  • cu = [cu1, cu2]
If u = u1i + u2j and v = v1i + v2j, then
  • 0 = 0i + 0j
  • –v = –v1i – v2j
  • u + v = (u1 + v1)i + (u2 + v2)j
  • u – v = (u1 – v1)i + (u2 – v2)j
  • cu = cu1i + cu2j
or, equivalently,
Calculations with components in 2-space Suppose u and v are vectors in 2-space and c is any scalar. In terms of components with respect to some coordinate system in 2-space,
Let's look first at how to do vector component calculations for vectors in 2-space.

The easiest vector to calculate is the zero vector - when its tail is at (0, 0), its head is as well, so its components are both 0:

0 = [0, 0]     or     0 = 0i + 0j.

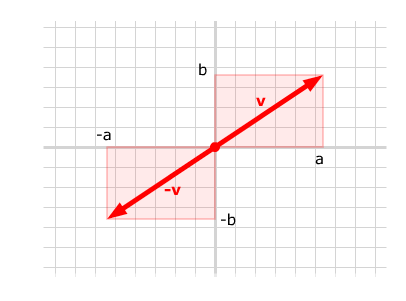
The next easiest to figure out is the negative of a vector - a little bit of triangle geometry shows that

if v = [a, b], then –v = [–a, -b]

or equivalently

if v = ai + bj, then –v = –ai – bj.

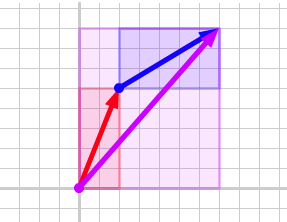
Next, let's look at the sum of two vectors in component form. Look at the boxes containing each vector and the sum. In the diagram below, the boxes contain two vectors (red and blue) and their sum (purple). The width and height of the box containing the purple vector are the sums of the widths and heights of the boxes containing the red and blue vectors.

This means that, to find the components of the sum, we just add the components of the individual vectors:

if u = [a, b] and v = [c, d], then u + v = [a + c, b + d] .

This is true for any pair of vectors in 2-space. In the diagram below, change the red and blue vector by dragging their heads and look at the widths and heights of their containing boxes. What happens if one or more of the components of the vector is negative?

You can also show this rule algebraically. Write the two vectors in i-j form:

u = ai + bj,    v = ci + dj.

Then

u + v = (ai + bj) + (ci + dj) .

Since vector addition is both commutative and associative, you can rearrange the sum in any order:

u + v = (ai + ci) + (bj + dj).

Then, using the first distributive rule, you get what you want:

u + v = (a + c)i + (b + d)j .

We can combine the component rule for sums with the component rule for negatives to get the component rule for subtraction: if u = ai + bj  and v = ci + dj, then

u - v = u + (-v) = (ai + bj) + (-ci - dj) = (a - c)i + (b - d)j

i.e. to find the components of the difference of two vectors, just subtract their individual components.

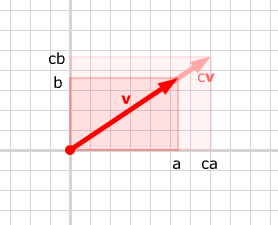
Scalar multiples are also easy to deal with in component form: if you scale a vector by a factor c, then its components also scale by that same factor c.

In symbols, if v = [a, b], then cv = [ca, cb].

You can also use algebra to derive this rule. If v = ai + vj, then

cv = c(ai + bj)
= c(ai) + c(bj)  
= (ca)i + (cb)j  
(using the second distributive rule)
(using the rule that the order of scalar multiplications doesn't matter)
If u = [u1, u2, u3] and v = [v1, v2, v3], then
  • 0 = [0, 0, 0]
  • –v = [–v1, –v2, –v3]
  • u + v = [u1 + v1, u2 + v2, u3 + v3]
  • u – v = [u1 – v1, u2 – v2,  u3 – v3]
  • cu = [cu1, cu2, cu3]
If u = u1i + u2j + u3k and v = v1i + v2j + v3k, then
  • 0 = 0i + 0j + 0k
  • –v = –v1i – v2j – v3k
  • u + v = (u1 + v1)i + (u2 + v2)j + (u3 + v3)k
  • u – v = (u1 – v1)i + (u2 – v2)j + (u3 – v3)k
  • cu = cu1i + cu2j + cu3k
or, equivalently,
Calculations with components in 3-space

Suppose u, v and w are vectors in 3-space and c is any scalar. In terms of components with respect to some coordinate system in 3-space,

 

The rules for calculating with vector components in 3-space are the same as those for calculating with vector components in 2-space, except that there is always one additional component to deal with. The lists of properties which follow summarize all the rules we've discussed in this section.