The determinant of a square matrix is built out of "signed elementary products" of the numbers in that matrix.

An elementary product of a square matrix is any product of its entries with exactly one entry from every row and every column. An n x n matrix has n! elementary products. Here's an example for n = 4.

 

Each elementary product has an associated sign which depends on the rows and columns its numbers come from. Here's how to find that sign.

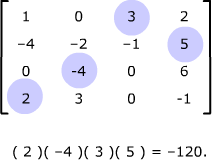
Suppose, for example, we look at the next to last elementary product in the example above and tabulate the positions of its component numbers.

Entry	3	5	–4	2
Row position	1	2	3	4
Column position	3	4	2	1

Transform the list of column positions by repeatedly swapping pairs of them until you match the list of row positions, and count the number of swaps you need.

Entry	3	5	–4	2
Row position	1	2	3	4
Column position	3	4	2	1
1.   3 ↔ 1  produces	1	4	2	3
2.   4 ↔ 2  produces	1	2	4	3
3.   3 ↔ 4  produces	1	2	3	4
Total number of swaps: 3

The sign of that elementary product is + if the number of swaps is even, or – if the number of swaps is odd. (The actual number of swaps you do or the order in which you do them turns out not to matter; for any given elementary product, you will either always get an even number of swaps, or always get an odd number of swaps.) In this case, the number of swaps (3) is odd, so the sign attached to the elementary product is –. The signed elementary product is then
–(–180) = 180.

In the interactive example above, the elementary products in pink have a + sign attached, and those in blue have a – sign attached.

Once we have the signed elementary products, we can define a determinant.

Given a square matrix A, the determinant of A is the number found by

• calculating all elementary products of A
• attaching the appropriate sign to each elementary product
• adding the results.

The determinant of A is denoted by det(A), or by replacing the brackets of A by straight lines: for example, if

then

.

Needless to say, calculating a determinant by using the formal definition would consume a horrendous amount of time, even for quite small matrices. In practice, we don't use the definition to calculate determinants, but we do use it to develop rules that help us calculate determinants more efficiently.