If we swap two rows of a determinant, we have the same elementary products as before, but to get the correct sign for each one, we'll need to do one extra swap of the row numbers to line them up with the column numbers. This extra swap changes the sign of each elementary product, so it changes the sign of the whole determinant.

The row operation Ri ↔ Rj changes the sign of the determinant.

 

 

Every elementary product of the original determinant contains exactly one entry from row i. Multiplying all those entries by c just multiplies the whole determinant by c.

The row operation Ri ← cRi,   c ≠ 0 multiplies the determinant by c.

 

 

The numbers in row i of this new determinant are sums, so we can split the determinant into the sum of two determinants. The first has row i in its original position, so it's just the determinant of the original matrix. The second has k times row j in that position. Since row j occurs elsewhere in the determinant, this second determinant has two proportional rows, and so is 0. The net result is no change to the original determinant.

The row operation Ri ← Ri – kRj,  j ≠ i doesn't change the value of a determinant.

As long as you keep track of the effects of the row operations you use, you can reduce a determinant to upper triangular form and then find its value by multiplying the numbers on the diagonal. Here's an example: suppose you wanted to calculate the value of the determinant

.

You notice that row one has a factor 2, so you want to apply the row operation R1 ← (1/2)R1. Doing so will multiply the determinant by 1/2, so you need to include an extra factor 2 to compensate.

.

(Notice that the net effect is to factor a 2 out of row one.) Now you want to get zeroes below the 1 in column 1. You use the row operations R2 ← R2 – R1 and R3 ← R3 – R1, which don't change the value of the determinant.

.

Next swap rows 2 and 3. This changes the sign of the determinant, so insert a minus sign to compensate:

.

Multiply row 2 by (-1). This multiplies the determinant by (-1), so to compensate, multiply the -2 out front by -1.

.

Now apply the row operation R4 ← R4 – 2R2. It doesn't change the value of the determinant, so you get

.

The determinant is now in upper triangular form, so its value is the produce of its diagonal elements. Your original determinant thus had value

2(1)(1)(6)(5) = 60.

A few more useful things to notice. Since the determinants of a matrix and its transpose are equal, you can use column operations to simplify a determinant if you wish: performing a column operation on a matrix has the same effect as performing the corresponding row operation on its transpose. Using Ci to denote column i for any i, the three column operations and their effect on determinants are

• Swap columns i and j: Ci ↔ Cj. Changes the sign of the determinant.
• Multiply a column by a non-zero constant: Ci ← cCi,   c ≠ 0. Multiplies the determinant by c.
• Replace a column by itself minus a multiple of another column: Ci ← Ci + kCj,    j ≠ i. Has no effect on the determinant.

Something to notice about the second type of elementary row or column operation: this one's most useful if you think of it as factoring a number out of a row or column of a determinant instead of as multiplication. For example, factor a 3 out of column three in the following determinant:

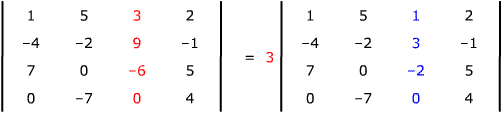
Caution: don't mix row and column operations in the same step. Here's a classic exam error – can you explain what the student did incorrectly?

Finally, we can use row operations to show the most important determinant property of all.

A matrix has an inverse if and only if its determinant is not zero.

Proof: Key point: row operations don't change whether or not a determinant is 0; at most they change the determinant by a non-zero factor or change its sign.

Use row operations to reduce the matrix to reduced row-echelon form.

If the matrix is invertible, you get the identity matrix, with non-zero determinant 1, so the original matrix had a non-zero determinant.

If the matrix is not invertible, its reduced row echelon form has a column without a leading 1. It has the same number of rows as columns, so at least one row is a row of zeroes. The determinant of the reduced matrix is 0, so the determinant of the original matrix is 0.

The most useful of those rules turns out to be the one for the determinant of a triangular matrix. Most determinants you'll want to calculate are not triangular; however, we do have a method for transforming a given matrix into triangular form: row reduction. (See the learning object How to Row Reduce a Matrix for details.)

 

A consequence. Suppose we then have a determinant with two equal rows. Swapping those rows doesn't change the determinant, but at the same time does change its sign. The only number unchanged by changing its sign is 0, so the determinant must be 0.

The value of a determinant with two equal rows must be 0.

A consequence. Suppose then we have a determinant with two proportional rows, say row j is c times row i. Multiplying row i by c then multiplies the whole determinant by c but creates a determinant with two equal rows, so the determinant must be 0 again.

The value of a determinant with two proportional rows must be 0.

The reduced row-echelon form of a square matrix must be upper triangular. If we can transform a matrix into reduced row-echelon form and account for the effect on the determinant of each row operation we use, we'll have an efficient method of calculating determinants of any size. Let's start by looking at how each of the three types of row operation affects a determinant.

The rules and properties developed on the previous page allow you to calculate particular types of determinant or to calculate a determinant from some related determinant. On their own however, they don't help much if you have to calculate a large determinant which doesn't have some special form.