There are two ways to add a pair of vectors.

Head-to-tail Rule.

Suppose you want to combine two displacement vectors geometrically. The obvious strategy is to start the second arrow where the first ends.

 

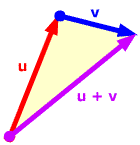
This is the basis of the triangle rule or head-to-tail rule for vector addition: position the tail of the second vector on the head of the first. Their sum has the tail of the first as its tail and the head of the second as its head.  

 

Tail-to-tail Rule

On the other hand, if you have two forces acting on the same object that you want to combine geometrically, a better choice would be to start both arrows at the the same point (the object).

 

This is the basis for he parallelogram rule or tail-to-tail rule for vector addition: position both vectors at a common tail. The two vectors form the sides of a parallelogram. Their sum lies along the diagonal of that parallelogram.

 

Fortunately, these rules give the same result: the triangle is half the parallelogram. In this diagram, the purple vector is the sum of the red and blue vectors. You can change the red and blue vectors by dragging their heads.

If one of the vectors you're adding is the zero vector, its head and tail coincide, so the result by either rule is the other vector: u + 0 = u or 0 + v = v.
Once we have an addition defined for vectors, we can define subtraction of vectors. First we need to know what the negative of a vector is.
The negative of a given vector has the same length as that vector, but the opposite direction.

The sum of any vector and its negative is the zero vector: v + (-v) = 0.  

To subtract a vector, we add its negative: u - v = u + (-v).

 

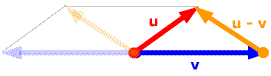
If we then shift u - v so its tail lies on the head of v, its head will lie on the head of u. 

 

Thus, if u and v have the same tail, u - v stretches from the head of v to the head of u. Another way to look at it: u - v is the other diagonal of the parallelogram formed by u and v. To get the direction of u - v right, make sure that v + (u - v) = u.  

What happens to the parallelogram rule when you're adding two parallel vectors?