To do anything more complicated than simple additions or scalar multiplications with geometric vectors, we need some calculation rules. Most of these rules are vector counterparts of the usual rules for calculating with scalars.
The first rule: vector addition is commutative: for any vectors u and v,
            u + v = v + u.

It's easy to see why; look at the parallelogram rule for addition. No matter which order we choose u and v in, their sum is just the diagonal of the parallelogram they form.

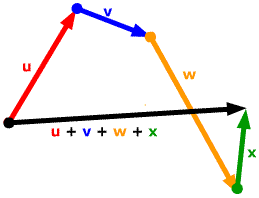
What if we want to add three or more vectors? The triangle rule (head-to-tail rule) suggests that we line them all up head to tail; then take as the sum the vector with the tail of the first vector and the head of the last.

The diagram shows the result of both sides of this calculation: the black vector.

You can change the vectors by dragging their heads.  

The vectors in the diagram need not all lie in the same plane; all our calculation rules work for vectors in 2-space or in 3-space.  

The rule above is correct, but vector addition is technically defined for two vectors only, so we have to make sure that the extended head-to-tail rule works even if we add the vectors two at a time. The rule we need: vector addition is associative, i.e. for any three vectors u, v, and w,
                       (u + v)+ w = u + (v + w)
By using the commutative rule and associative rule over and over, we can add any number of vectors in any order. There is a useful visual representation of the sum of three vectors which shows this: a generalization of the parallelogram rule called the parallelepiped rule.

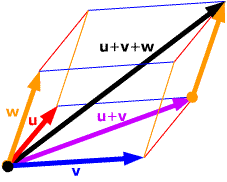
A parallelepiped is a three-dimensional solid with all of its faces parallelograms. Suppose we have three vectors which don't all lie in a plane. Place them all tail-to-tail and make them into the edges of a parallelepiped, as in the diagram.

If we use the parallelogram rule to find u + v and then the triangle rule to find (u + v)+ w, we get a vector from one corner of the parallelepiped to the opposite corner. We could have started with any other pair of vectors; the result will still be the same vector between the two opposite corners.

In other words, the sum of three vectors not all in a plane is the diagonal of the parallelepiped they form.

Suppose now that we have two scalars c and d multiplying a vector v; does it matter in which order we do the multiplication? It turns out not to: the order of scalars in scalar multiplication is irrelevant: c(dv) = d(cv) = (cd)v.

If c and d are positive, this is easy to see: the result in all three calculations is just a vector with length cd times the length of v and the same direction as v. If either or both of c and d are negative, we have to take direction reversals into account, but there are always the same number of reversals in each part of the calculation, so the rule still works.

Whenever we have some sort of addition and multiplication together, we have possible distributive rules. In fact, since we are multiplying two different sorts of objects (scalars and vectors) we have two distributive rules. It all depends on where the sum occurs.
If we have the sum of scalars times a vector, we have the rule: scalar multiplication is distributive over the sum of scalars. Symbolically, for any scalars c and d and any vector v,
          (c + d)v = cv + dv.

If c and d are positive (as in the diagram), this is easy to see visually: the result for both sides of the calculation is a vector with length c + d times the length of v and the same direction as v.

If either or both of c and d are negative, the same basic idea still works, but some of the vectors have the opposite direction, which needs to be accounted for.

The way to think of this rule is to think of scalar multiplication as scaling the vector. The rule says that if you scale two vectors by the same amount, then you also scale their sum by that amount.

In the diagram, you can change the value of the scalar c with the slider, and you can change the vectors u and v (the darker red and blue ones) by dragging their heads.

If we have a scalar times a sum of vectors, we have another distributive rule: scalar multiplication is distributive over the sum of vectors. Symbolically , for any scalar c and any vectors u and v,
                                               c(u + v) = cu + cv.

 

Geometric Vectors
Introduction Representing geometric vectors Adding geometric vectors Multiplying geometric vectors by scalars Calculation rules for addition and scalar multiplication