 Geometric
Vectors Geometric
Vectors |
||||
| Introduction | Representing geometric vectors | Adding geometric vectors | Multiplying geometric vectors by scalars | Calculation rules for addition and scalar multiplication |
 To
represent a vector geometrically, we use arrows (also known as "directed
line segments"). The length of the arrow represents the vector's
size, and its direction represents the vector's direction in 2-space or in
3-space.
To
represent a vector geometrically, we use arrows (also known as "directed
line segments"). The length of the arrow represents the vector's
size, and its direction represents the vector's direction in 2-space or in
3-space.
For example , we could represent a displacement 2 km southwest by the arrow in the diagram.
Vectors are parallel if their shafts are parallel. They must have either the same direction or opposite directions, but can have any length.

Though it has no direction, the zero vector is thought of as being parallel to every vector.
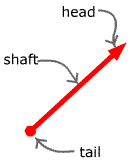 To describe a vector, we refer to its tail (more
formally: its initial point), its head (more
formally: its terminal point) and its shaft.
To describe a vector, we refer to its tail (more
formally: its initial point), its head (more
formally: its terminal point) and its shaft.
Use a single letter with an arrow:

It's difficult to write boldface with a pencil or pen, so the single letter with arrow is used more for handwritten materials like classroom notes.
The "head-point to tail-point" form is often used when the vector joins previously named points. However, it is difficult to reproduce this notation on a web page, so instead, we'll omit the arrow and just use boldface letters, like AB.
Use a single boldface letter:

Use the names of its head and tail with an arrow:

If you change an arrow by dragging its head or tail, you change the relation between the head and tail, so you change the vector the arrow represents.