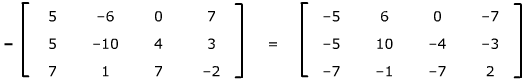Matrices can be added or subtracted only when they have the same size.

To add or subtract two m x n matrices, add or subtract their corresponding entries.

 

 

A zero matrix is one of any size all of whose entries are 0. Notation: Omxn if it's important to indicate the size, O if the size is unimportant or clear from the context.

For any matrix A, A + O = A and O + A = A.

The negative of a matrix is the matrix whose entries are the negatives of the original matrix.

For any matrix A, A + (-A) = O

To multiply a matrix by a scalar, multiply every entry of the matrix by that scalar.

There are two distributive rules for scalar multiplication:

For any m x n matrices A and B and any scalar c,

c(A + B) = cA + cB

For any m x n matrix A and any scalars c and d,

(c + d)A = cA + dA.

These rules work because they work for number addition and multiplication - you're just doing the calculation "in bulk" again.

If you take an extended combination of sums and scalar multiples of matrices of the same size, you get a linear combination.

A linear combination of several matrices A1, A2, ..., Ak of the same size is any matrix of the form

c1A1 + c2A2 + ... + ckAk

where c1, c2, ..., ck are all scalars.

For example, if A, B, C and D are all 2 x 3 matrices, then the 2 x 3 matrix

3A – 2B – 5C + D

is a linear combination of A, B, C and D. So is

3(A + 2B) – 4C + 5(D – A + C) – B,

since you can simplify this expression to –2A + 5B + C + 5D.

You can think of addition and subtraction as "bulk" addition or subtraction - you're just doing nm additions or subtractions instead of 1. Matrix addition and subtraction obey most of the same rules as number addition and subtraction, for example:

Matrix addition is commutative: for any m x n matrices A and B,
                   A + B = B + A.

Matrix addition is associative: for any m x n matrices A, B and C,
                  A + (B + C) = (A + B) + C.

Scalar multiplication. A scalar is just another word for number (to distinguish numbers from other mathematical objects we want to calculate with).