A matrix is a rectangular array of numbers enclosed
in brackets, for example
.
You may already have seen linear systems of equations solved by operating on the rows of the augmented matrix of the system. In this learning object, we're going to look at operations you can do on matrices as a whole, instead of just on individual rows. Specifically, we'll look at
- How to add and subtract matrices, how to multiply them by scalars, and the calculation rules for these operations,
- How to multiply two matrices, and how matrix multiplication differs from ordinary number multiplication,
- Why we can't generally divide matrices, what the inverse of a matrix is, and how to find it.
An m x n
matrix A is a rectangular array of
numbers with m rows and n columns. The numbers are called the entries of A.
A row matrix is one with a single row.
![]() .
.
A column matrix is one with
a single column. ![]()
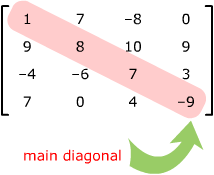
A square matrix is one with the same number of rows as columns. Entries of a square matrix with the same row and column numbers lie along its main diagonal.
Prerequisites. None, except for the last page. For that, you should know
how to reduce a matrix to reduced row-echelon form, and the connection between
row reduction and the solution of linear systems. See the learning objects
How to Row Reduce a Matrix and Solving
Linear Systems for further information
on these topics.
Keywords: matrix addition, zero matrix, negative of a matrix, matrix scalar
multiplication, identity matrix, inverse of a matrix
Before we begin, here's a little matrix vocabulary
you'll need to understand the pages that follow.
Matrices and Matrix Calculations |
|||
| Introduction | Addition, subtraction and scalar multiplication | Multiplying matrices | The inverse of a matrix and how to find it. |
