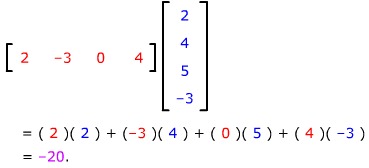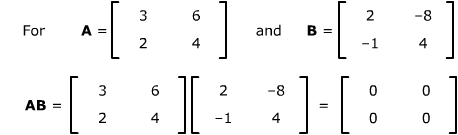Multiplying matrices is a bit more complicated
than "bulk multiplication" - you
don't just multiply the corresponding entries of the matrices.
The simplest matrices to multiply are a row matrix
and a column matrix, provided they have "matching sizes" - the "width" of
the row must be the same as the "height" of the column.
To multiply a 1 x n row matrix by an n x 1 column matrix, in
that order:
- multiply their corresponding entries together
- add the results.
For example,
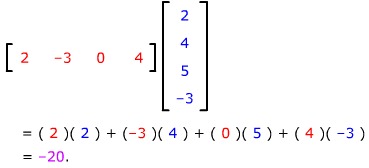
You can think of this product as either a scalar or a 1 x 1 matrix.
Notice that the order of the matrices you're multiplying
is important, since you always use rows from the first matrix and columns
from the second. The two matrices above cannot be multiplied in the opposite
order.
Here's an example.
Unlike addition and scalar multiplication, matrix
multiplication does not obey all the same rules that number multiplication
does. We're now going to look at examples of which calculation rules work as
they do for numbers and which calculation rules don't.
Matrix multiplication is
NOT commutative: for most matrices
A and
B,
AB ≠
BA,
even when both products are defined and are the same size.
Example:

Thus AB ≠ BA.
Matrix multiplication IS
associative:
for
any matrices
A,
B and
C with
appropriate matching sizes,
(AB)C = A(BC).
This is not obvious - a proof of some sort is needed but will be omitted
here.
Multiplication by a zero
matrix gives a zero matrix: for any m x
n matrix
A,
OkxmA = Okxn and AOmxj = Onj
A zero matrix thus performs the same function for multiplication as the
number 0 does for number multiplication. Notice that you generally need a
different size zero matrix to multiply A on each side.
For numbers,
multiplication of any number by 1 doesn't change that number. The matrices
that perform this function for matrix multiplication are the
identity
matrices.
Identity matrices are square matrices with 1's along the main diagonal
and 0's everywhere else – for example, the 2 x 2 identity matrix is
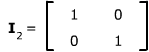 .
.
The n x n matrix is written as In,
or just I if the size is not important or
is clear from the context.
If A is any m x n matrix, then ImA = A and AIn = A.
(Notice that you generally need different size identity matrices to multiply
A on different sides.)
Matrix multiplication IS
distributive: for any matrices
A,
B and
C for
which the sums and products are defined
A(B + C)
= AB + BC and (B + C)A = BA + CA.
Notice that you need two distributive rules, one for the sum on the left
and the other for the sum on the right. Since matrix multiplication is not
commutative, these rules say different things.
Cancellation in matrix
multiplication DOES NOT work: for most matrices
A,
B and
C with
AB =
AC,
in general,
B ≠
C even
if
A ≠
O.
Example:

So AB = AC but B ≠ C.
If the product of two matrices is a zero matrix,
it does NOT follow that one of the matrices has to be a zero matrix.
Example:
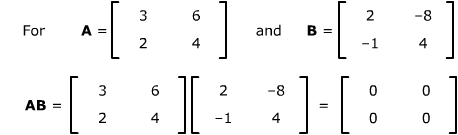
So AB = O but
neither A nor B is
a zero matrix.
Square matrices can always be multiplied by themselves, so you can talk
about their powers; for example
A4 =
AAAA.
As you would expect, the power
A0 is
defined to be the "1" for matrix multiplication,
i.e.
A0 =
I.
You can also talk about polynomials of square matrices – expressions
such as 3A2 – 2A +
5I, for example.
The "matching sizes" condition must hold when you multiply more
general matrices as well: the "width" of the first has to be the
same as the "height"
of the second. Once that's true, you can multiply more general matrices just
by multiplying all the rows of the first by all of the columns of the second.
With caution, you can carry out many algebraic calculations with
matrices as you do with numerical variables. However, even for square matrices,
many common algebraic identities don't work. For example, the usual formula
for squaring a binomial doesn't work because, for any same-sized square
matrices
A and
B,
(A + B)2 = (A + B)(A + B)
= A(A + B)
+ B(A + B)
= A2 + AB + BA + B2,
which does not equal A2 + 2AB + B2 unless AB = BA.
To form the product of an m x n matrix
A and
an n x k matrix
B:
- The product AB is an m x k matrix.
- The entry in row i and column j of AB is
the product of row i of A and column j of B.
Does the difference of squares factoring work
for matrix multiplication? i.e., given two matrices
A and
B of
the same size, does
A2 – B2 =
(A + B)(A – B)
?
.